filmov
tv
If AA + BB + CC = ABC, What Are A, B and C?

Показать описание
If AA + BB + CC = ABC, what are the values of A, B, and C? All the digits are distinct and positive. Watch the video for a solution.
Connect on social media. I update each site when I have a new video or blog post, so you can follow me on whichever method is most convenient for you.
My Books
Connect on social media. I update each site when I have a new video or blog post, so you can follow me on whichever method is most convenient for you.
My Books
If AA + BB + CC = ABC, What Are A, B and C?
Maths Problem: AA+BB+CC=ABC | How to Solve It
If AA+BB+CC=ABC, What are A, B, and C? | Minute Math
If aa+bb+cc=abc then find the value of a, b, c?
#ZESTFORSCIENCE IF AA+BB+CC=ABC, THEN LET'S KNOW WHAT ARE THE NONZERO VALUES OF A,B,C.
If AA +BB+CC is ABC then A=?? #shorts #mathstricks
If AA+BB+CC=ABC What are A,B,C.
AA+BB+CC=ABC ¿Cómo se resuelve? 🤔
Aa - Bb - Cc - Dd ..... - Zz
If AA + BB + CC = ABC, then Find A, B and C
How to Write Letters Aa, Bb, Cc, Dd, Ee, Ff--fast
If AA+BB+CC=ABC then A=? B=?C=? maths tricks
Writing english capital and small letter | Print handwriting | Aa Bb Cc Dd | Handwriting Learning
How to WRITE English Alphabet Letters Aa Bb Cc !!!!!! Uppercase and Lowercase
maths tricks If AA+BB+CC=ABC then A=? B=?C=? #shorts
If AA+BB+CC = ABC l Then A = ?, B =?, C =? l Ritvik JAS l Comment l Please Subscribe 🙏🙏 🙏🥰😭...
SOLVE THIS PUZZLE | AA + BB + CC = ABC | ANC + ABC + ABC = BBB | ABC + ABC + ABC = CCC |
AA + BB + CC = ABC II Find A, B, C
Can you Solve this? | AA + BB + CC = ABC | @thenumberverse
Aa Bb Cc Song
Aa Bb Cc Dd English Alphabets For Beginners//Alphabet Writing//Capital And Small Letter Writing||
ABC Song - Learn English Alphabet for Children with Diana
The ABC Song | CoComelon Nursery Rhymes & Kids Songs
o no no 😂 #shorts #viral #funny #comedy @ateetkxyz
Комментарии
 0:03:25
0:03:25
 0:08:26
0:08:26
 0:05:19
0:05:19
 0:01:04
0:01:04
 0:04:13
0:04:13
 0:00:06
0:00:06
 0:08:50
0:08:50
 0:03:21
0:03:21
 0:00:17
0:00:17
 0:05:31
0:05:31
 0:01:46
0:01:46
 0:07:13
0:07:13
 0:02:52
0:02:52
 0:06:02
0:06:02
 0:00:25
0:00:25
 0:00:11
0:00:11
 0:00:56
0:00:56
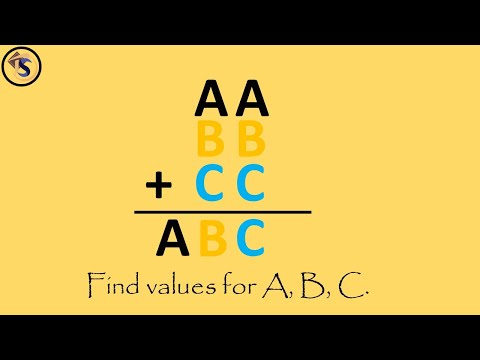 0:03:58
0:03:58
 0:02:44
0:02:44
 0:00:07
0:00:07
 0:02:18
0:02:18
 0:04:51
0:04:51
 0:03:52
0:03:52
 0:00:16
0:00:16