filmov
tv
Can They Crack THIS Logarithmic Equation? Math Olympiad Challenge
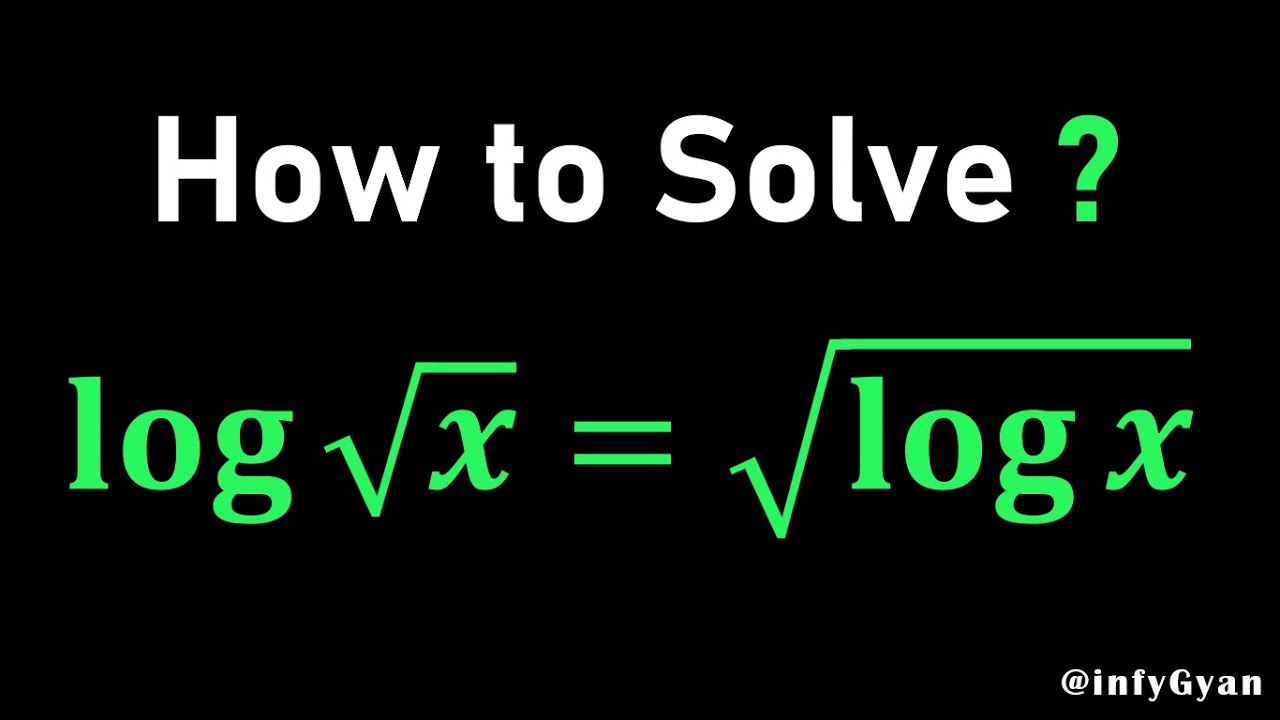
Показать описание
Can They Crack THIS Logarithmic Equation? Math Olympiad Challenge
In this video, we're taking on the math Olympiad challenge: can they crack the logarithmic equation? Watch as we work our way through the equations!
The math Olympiad challenge is a fun way to challenge your brain and test your skills in mathematics. In this video, we're taking on the logarithmic equation, one of the more challenging puzzles in the math Olympiad. Can you help us solve the puzzle before time runs out?
Topic Covered:
1) Logarithmic equations
2) Math Olympiad
3) Logarithm problems
4) Math competition
5) Logarithm techniques
6) Math tutorial
7) Advanced math
8) Problem-solving
#logarithms #matholympiad #mathcompetition #mathtutorial #problemsolving #advancedmaths #MathSkills #mathematics
7 Key moments of this Video:
0:00 Introduction
0:37 Natural log
0:59 Properties of logarithm
1:28 Substitution
2:34 Factorization
3:00 Finding solutions
4:10 Verify results
Channel link for more perks:
Useful Links:
Thanks for watching video!!
@infyGyan
In this video, we're taking on the math Olympiad challenge: can they crack the logarithmic equation? Watch as we work our way through the equations!
The math Olympiad challenge is a fun way to challenge your brain and test your skills in mathematics. In this video, we're taking on the logarithmic equation, one of the more challenging puzzles in the math Olympiad. Can you help us solve the puzzle before time runs out?
Topic Covered:
1) Logarithmic equations
2) Math Olympiad
3) Logarithm problems
4) Math competition
5) Logarithm techniques
6) Math tutorial
7) Advanced math
8) Problem-solving
#logarithms #matholympiad #mathcompetition #mathtutorial #problemsolving #advancedmaths #MathSkills #mathematics
7 Key moments of this Video:
0:00 Introduction
0:37 Natural log
0:59 Properties of logarithm
1:28 Substitution
2:34 Factorization
3:00 Finding solutions
4:10 Verify results
Channel link for more perks:
Useful Links:
Thanks for watching video!!
@infyGyan
Can They Crack THIS Logarithmic Equation? Math Olympiad Challenge
'Crack This Logarithmic Puzzle: Can You Solve It?'
Logarithmic Challenge Can You Crack the Code of This Complex Fraction #maths
Oxford student reacts to India’s JEE Advanced exam paper *really hard* #shorts #viral #jeeadvanced
Logarithmic Brain Teaser: Can You Solve This Equation and Impress Your Friends?
A Challenging Logarithmic Inequality
Solving IIT-JEE question in 30 seconds!!
Find the Correct Option(s) for this Logarithmic Quiz! 🤔 #shorts #algebra #math #logarithm #maths
IITian Fun - Logarithmic Humour 😅😅😅 - #jee2023 #namokaul #purnimakaul #jee #unacademyjee
USA OLYMPIAD | Solve the Logarithmic equation 💨 find the value of x
A Nice Logarithmic Problem | Solve for x ? | Logarithms
How to Solve Logarithmic Equations
𝗖𝗹𝗮𝘀𝘀 𝟭𝟬: 𝗖𝗿𝗮𝗰𝗸 𝗟𝗼𝗴𝗮𝗿𝗶𝘁𝗵𝗺𝗶𝗰 𝗧𝗶𝗺𝗲 𝗖𝗼𝗺𝗽𝗹𝗲𝘅𝗶𝘁𝘆 (𝗢(𝗹𝗼𝗴 𝗡)) 𝗶𝗻 𝗣𝘆𝘁𝗵𝗼𝗻 | 𝟮𝟬𝟮𝟰 𝗗𝗦𝗔 𝗖𝗼𝘂𝗿𝘀𝗲...
Crack the Code Mastering MIT Integration Bee with Logarithmic Leverage!
Solving Complex Logarithmic Equations of different Bases | Can you solve for X?
Solving an Exponential Equation with Logarithmic Indices
Solving logarithmic equations
Logarithmic Series|| Very Important Problems on Logarithmic Series || Logarithmic Series ||
💡 Trivia Tuesday: Logarithmic Challenge
Exponential and Logarithmic Past Paper Questions
Logarithms - Basics | What are Logs? | Don't memorise | The Easy Way | Logarithmic Function
Solve a logarithmic equation. Japanese Mathematical Competition.
Solving Logarithmic Equations (challenging)
Solving Logarithmic Equations #shorts #youtubeshorts #shortsfeed #math
Комментарии
 0:07:21
0:07:21
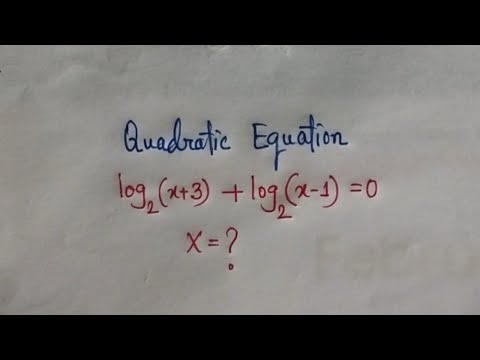 0:10:46
0:10:46
 0:00:45
0:00:45
 0:01:00
0:01:00
 0:04:03
0:04:03
 0:02:03
0:02:03
 0:00:29
0:00:29
 0:00:59
0:00:59
 0:00:18
0:00:18
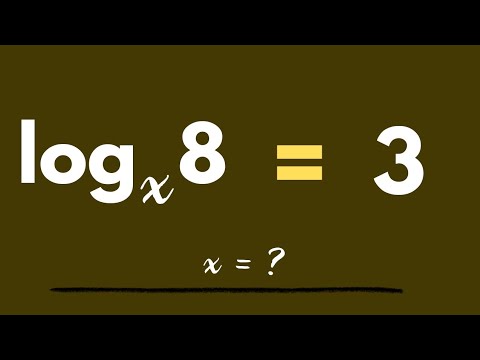 0:04:01
0:04:01
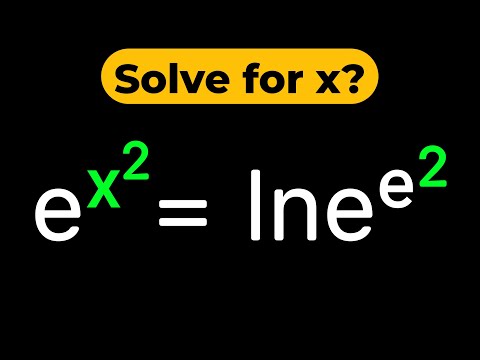 0:01:57
0:01:57
 0:05:10
0:05:10
 0:34:46
0:34:46
 0:01:25
0:01:25
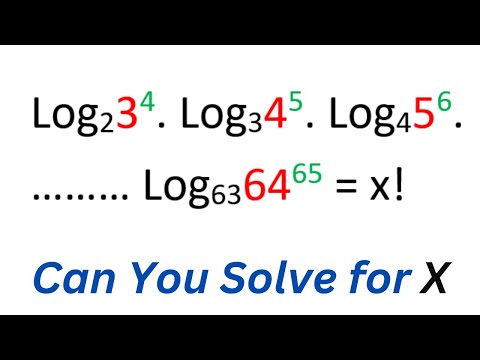 0:05:57
0:05:57
 0:01:00
0:01:00
 0:11:27
0:11:27
 0:33:03
0:33:03
 0:01:21
0:01:21
 0:08:51
0:08:51
 0:00:17
0:00:17
 0:04:59
0:04:59
 0:04:11
0:04:11
 0:00:55
0:00:55