Dot products, Pythagoras' theorem, and generalizations | Wild Linear Algebra A | NJ Wildberger

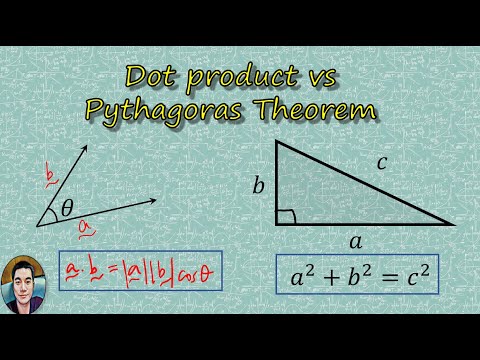
Here we begin to study metrical geometry from the framework of linear algbra, but we do so in a novel, completely algebraic way. The starting point is the dot product, motivated by Pythagoras' theorem but logically independent of any prior understanding of Euclidean geometry.

The main properties of the dot product are that it is bilinear and symmetric. From the dot product we define perpendicularity of vectors, and the quadrance of vectors, which replaces the `length' and is a purely algebraic quantity--so much more general, accurate and allowing us to work over the rational numbers as usual.

Pythagoras' theorem then gets a completely algebraic proof, which is quite fundamental. This topic should be a cornerstone of all undergraduate linear algebra courses (and of course in the future it will be!)

Finally we introduce the idea of more general symmetric bilinear forms, associated to symmetric 2x2 matrices. These will allow us to extend much of this discussion, in particular to understanding the relativistic geometry introduced a century ago by Einstein and Minkowski.

Video Chapters

00:00 Introduction
3:30 The fundamental dot product of vectors
08:22 Symmetric property of the dot product
15:05 Pythagoras Theorem via Linear Algebra
24:17 Transpose

*************************

Here are the Insights into Mathematics Playlists:

Here are the Wild Egg Maths Playlists (some available only to Members!)

************************

[pickeyberry]

Video Content

00:00 Introduction
08:22 symmetric property
15:05 Thm(pythagoras)
24:17 Transpose

[rolfdoets]

Norman, you are a very good and nice teacher. The material of all your lectures is super stuff! .... I can't work them all through.... maybe now... because of Corona.... and what is your diet (breakfast&lunch) or secret?... the amount of energy is overwelming... again and again... Wonderfull to see

[adgut-gar]

The origin of the world inequality is simple and it´s easy to calculate (Another Pythagorean Theorem):
 
Modern world is ruled by the great oligarchies: businessmen, merchants, politicians, clerics, and army. They and their fans keep half of humanity in misery on behalf of their insane privileges, and they are corrupting and devastating the whole planet.
 
“Do not dream of the vanity of becoming rich, because you will increase the poor”: Pythagoras, 6th century B.C.
 
Actually these five castes and their henchmen, have only two option: change their behavior trying to repair the destruction and suffering they are causing, or pray for God does not exist, because, if He exists, surely He is engaged in preparing for them precious luxury suites in Hell. 
 
"Money can´t buy Heaven": Martin Luther, 1517.
 
As Pythagoras well calculated, if there exist poor people, it is because there exist rich people, so: What is the right price of goods and services?  The answer is …..
 
(To read the complete writing follow the link: “Ad Gut-Gar-Google+” in your browser. There, choose the button: “About”, and the writing is in “Story”)