filmov
tv
Limit comparison test (ln(n)/n)^2. Weird comparison 1/n^(3/2) explained by looking at 1/n and 1/n^2.

Показать описание
Questions or requests? Post your comments below, and I will respond within 24 hours.
We test the convergence of (ln(n)/n)^2 with a weird limit comparison test with L'Hopital's rule, including the motivation for limit comparison to 1/n^(3/2).
This limit comparison seems weird, but we motivate the successful comparison by looking at two inconclusive comparisons: one limit comparison to the harmonic series and one limit comparison to 1/n^2. Both of these are inconclusive for opposite reasons -- our terms are smaller than the divergent series, but larger than the convergent series. Finally, we try a comparison in between: the weird comparison 1/n^3/2 and we successfully show that the series converges by the limit comparison test.
Limit comparison test (ln(n)/n)^2. Weird comparison 1/n^(3/2) explained by looking at 1/n and 1/n^2.
Sum (ln(n)/n^2) weird limit comparison to 1/n^(3/2) motivation. L'Hopital's rule limit co...
10.6j Limit Comparison Test, Infinite Series, ln(n)/n^(7/2), Example - AP Calculus BC
Limit Comparison with SUM ln(n)/n^3 (Convergent or Divergent Series 23)
Determine whether series converges or diverges (ln n)/n. Use appropriate test
3 Decreasing Series ln n over n
Integral Test vs. Comparison Test: ln(n)/n^2 vs ln(n)/n^4
Alternating Infinite Sum of ln(n)/n^2
Calculus 2: Solving Exam 3 -All things SEQUENCES & SERIES! -Fall 2019 Part 1| Math with Profess...
Comparison Test | Series Converges or Diverges | Sum 1/ln(n) , n= 2 to infinity
Infinite Series Sum (ln(n/2))
Infinite Series SUM( ln(n/(2n + 5) ) || Does it Converge or Diverge?
Direct comparison test 1/(ln(n)), including derivative proof that ln(n) is less than n. Sum 1/ln(n).
Series ln n /e^n as n approaches to infinity Converges or Diverges Math Proof |Mad Teacher
Sum from n=2 to infinity of 1/(ln n)^(ln n)
Determine if sequence converges or diverges, if converges find limit {(ln n)^2/n}
Determine if series is absolutely, conditionally convergent or divergent { (-2)^n/(n ln n) }
Does the Series SUM(ln(n/(2n + 5)) Converge or Diverge?
100 series convergence tests (no food, no water, no stop)
Series Convergence Integral Test lnn / n
Calculus- Series (-1)^n/(n ln^2(n)) (integral test)
Determine the convergence or divergence of the series (n ln n)/ (2^n). Ratio Test. L’Hopital’s Rule...
Sum from n=1 to infinity of ln(n)/n!
Calculus Help: Divergent and Convergent- Summation 2(ln n)^3 / n - (Part 2) - Integral Test
Комментарии
 0:06:26
0:06:26
 0:03:43
0:03:43
 0:01:00
0:01:00
 0:02:48
0:02:48
 0:01:52
0:01:52
 0:03:58
0:03:58
 0:15:46
0:15:46
 0:14:01
0:14:01
 1:05:21
1:05:21
 0:00:49
0:00:49
 0:01:44
0:01:44
 0:03:24
0:03:24
 0:03:12
0:03:12
 0:04:41
0:04:41
 0:01:44
0:01:44
 0:02:16
0:02:16
 0:03:39
0:03:39
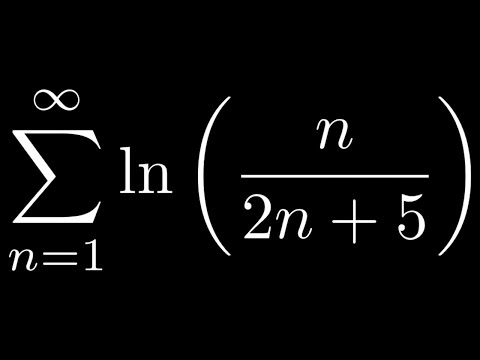 0:02:48
0:02:48
 6:06:54
6:06:54
 0:04:04
0:04:04
 0:02:33
0:02:33
 0:03:29
0:03:29
 0:01:40
0:01:40
 0:01:01
0:01:01