filmov
tv
General Relativity Lecture 9

Показать описание
(November 26, 2012) Leonard Susskind derives the Einstein field equations of general relativity and demonstrates how they equate spacetime curvature as expressed by the Einstein tensor, with the energy and momentum within that spacetime as expressed by the stress-energy tensor.
This series is the fourth installment of a six-quarter series that explore the foundations of modern physics. In this quarter Susskind focuses on Einstein's General Theory of Relativity.
Originally presented in the Stanford Continuing Studies Program.
Stanford University:
Stanford Continuing Studies Program:
Stanford University Channel on YouTube:
This series is the fourth installment of a six-quarter series that explore the foundations of modern physics. In this quarter Susskind focuses on Einstein's General Theory of Relativity.
Originally presented in the Stanford Continuing Studies Program.
Stanford University:
Stanford Continuing Studies Program:
Stanford University Channel on YouTube:
General Relativity Lecture 9
General Relativity Lecture 9: Energy Momentum Tensor and Equivalence Principle Primer
General Relativity Lecture 9
Special Relativity | Lecture 9
9. Acceleration and Geodesics (General Relativity)
Lecture 9: Newtonian spacetime is curved! (International Winter School on Gravity and Light 2015)
General Relativity, Lecture 9: parallel transport continued and geodesics
PHS3131 Special Relativity Lecture 9 David Paganin
General Relativity Topic 9: Densities and the Energy-Momentum Tensor
General Relativity, Lecture 9: Covariant Derivatives, Integration.
What is General Relativity? Lesson 9: Parallelism and the Covariant Derivative
General Relativity, Lecture 9
General Relativity: Lecture 9: Lagrangian Mechanics
What is General Relativity? Lesson 60: Scalar Curvature 9: Interpretation of Scalar Curvature
General Relativity Lecture 10
General Relativity (HEP-GR) Lecture 9
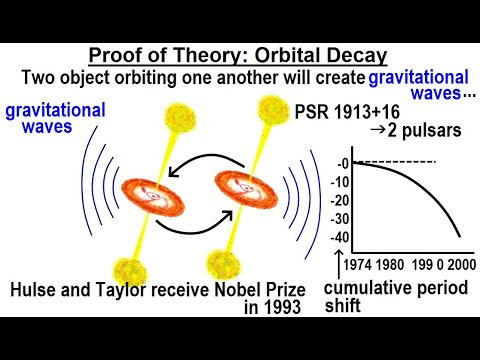
Astronomy - General Relativity (9 of 17) Proof of Theory: Orbital Decay
9 General Relativity Geodesic Equation as a Consequence of the Field Equation
General Relativity I (HEP-GR_I) Lecture 9
General Relativity Lecture, 9 December
General Relativity 9.a: Contractions and symmetries of Reimann
Simple Relativity - Understanding Einstein's Special Theory of Relativity
General Relativity Explained simply & visually
General Relativity Seminar 9/17/2021
Комментарии
 1:44:24
1:44:24
 1:10:45
1:10:45
 1:19:39
1:19:39
 1:39:52
1:39:52
 0:59:14
0:59:14
 1:48:32
1:48:32
 1:28:07
1:28:07
 0:50:47
0:50:47
 1:17:43
1:17:43
 1:20:13
1:20:13
 1:07:38
1:07:38
 1:52:10
1:52:10
 0:42:09
0:42:09
 0:51:48
0:51:48
 1:36:20
1:36:20
 1:36:34
1:36:34
 0:06:26
0:06:26
 0:26:01
0:26:01
 1:29:29
1:29:29
 1:29:31
1:29:31
 0:19:24
0:19:24
 0:05:56
0:05:56
 0:14:04
0:14:04
 0:56:58
0:56:58