filmov
tv
Spiral of Theodorus

Показать описание
This is a short, animated visual proof demonstrating how to construct square roots of any positive integer using the Spiral of Theodorus
Thanks!
#manim #math #mathshorts #mathvideo
#construction #geometry #mtbos #manim #animation #theorem #pww #proofwithoutwords #visualproof #proof #iteachmath #spiral #theodorus #squareroot
To learn more about animating with manim, check out:
Thanks!
#manim #math #mathshorts #mathvideo
#construction #geometry #mtbos #manim #animation #theorem #pww #proofwithoutwords #visualproof #proof #iteachmath #spiral #theodorus #squareroot
To learn more about animating with manim, check out:
Spiral of Theodorus Constructs Square Roots (visual proof; straightedge and compass)
Spiral of Theodorus
DIY Square Root Spiral Tutorial! #shorts
Spiral of Theodorus - Geogebra Live Build
Spiral of Theodorus | A SelfCAD Interactive Tutorial
Python Day 13: Beginning the Spiral of Theodorus
Spiral of Theodorus 😍🌀#shorts #spiraloftheodorus #mathematics #geometry
Constructing Square Root Spiral And Some Tips ~ Spiral of Theodorus ~ Theory explained too!
How to draw a Square Root Spiral
Tutorial : How to Construct a dynamic Theodorus Spiral with GeoGebra
Spiral of Theodorus #mathematics #pythagoreantheorem #geometry #spiral
Spiral of Theodorus
The Square Root Spiral 🌀 #learning #maths #shorts
How to make a Theodorus Spiral
Day 9: The Spiral of Theodorus!
The spiral of theodorus explained
Spiral of Theodorus
Spiral of theodorus on GeoGebra
Spiral Of Theodorus Explained
Spiral of THEODORUS
Progression of roots. Theodorus’ spiral
MathLapse - Spiral of Theodorus
Root Spiral of Theodorus
Teodoro Spiral [math] #mathematics #maths #math #physics #science #shorts #reels
Комментарии
 0:02:33
0:02:33
 0:00:52
0:00:52
 0:00:20
0:00:20
 0:20:59
0:20:59
 0:17:39
0:17:39
 0:11:06
0:11:06
 0:00:15
0:00:15
 0:12:04
0:12:04
 0:05:08
0:05:08
 0:11:04
0:11:04
 0:00:17
0:00:17
 0:05:13
0:05:13
 0:01:00
0:01:00
 0:03:27
0:03:27
 0:00:52
0:00:52
 0:00:38
0:00:38
 0:04:25
0:04:25
 0:02:57
0:02:57
 0:00:57
0:00:57
 0:00:45
0:00:45
 0:00:43
0:00:43
 0:02:14
0:02:14
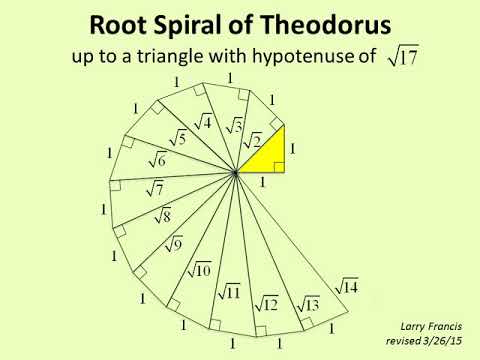 0:04:13
0:04:13
![Teodoro Spiral [math]](https://i.ytimg.com/vi/8DngImcVQvA/hqdefault.jpg) 0:00:18
0:00:18