filmov
tv
Limit at Vertical Asymptote

Показать описание
High school math teacher explains how to evaluate limits at a vertical asymptote!
After direct substitution of a limit, do you get a nonzero value divided by 0? If so, there is a vertical asymptote at that value of x! The answer to the limit must be infinity, negative infinity, or does not exist. Watch this video to see how to determine the answer to the limit!
Thank you for watching! Please comment below about any questions or comments you have about the problem discussed!
After direct substitution of a limit, do you get a nonzero value divided by 0? If so, there is a vertical asymptote at that value of x! The answer to the limit must be infinity, negative infinity, or does not exist. Watch this video to see how to determine the answer to the limit!
Thank you for watching! Please comment below about any questions or comments you have about the problem discussed!
Infinite Limits and Vertical Asymptotes
Limits approaching a Vertical Asymptote
Limit at Vertical Asymptote
Finding vertical and horizontal asymptotes using limits
How To Find The Vertical Asymptote of a Function
Evaluate the limits from a graph with horizontal and vertical asymptotes
Infinite Limit - Vertical Asymptote | Calculus | Math Video Central
Infinite limits and asymptotes | Limits and continuity | AP Calculus AB | Khan Academy
General Mathematics | ASYMPTOTES (Vertical & Horizontal) OF RATIONAL FUNCTIONS | Grade 11
Infinite Limits & Vertical Asymptotes Calculus 1 AB
How to Calculate Limits at Vertical Asymptote in Rational Functions Calculus
Understanding Limits - Vertical Asymptote
Ex 1: One-Sided Limits and Vertical Asymptotes (Rational Function)
Finding Vertical and Horizontal Asymptotes using Limits
Connecting Infinite Limits and Vertical Asymptotes
Visually determining vertical asymptotes | Limits | Differential Calculus | Khan Academy
02 One Side Limit and vertical Asymptote
1.14a Connecting Infinite Limit and Vertical Asymptotes
Limits (Vertical Asymptotes and Trigs)
Limits at Infinity & Horizontal Asymptotes
Connecting Infinite Limits and Vertical Asymptotes, Example - AP Calculus AB/BC
finding vertical asymptotes of rational functions, using limits
Infinite Limits: Horizontal and Vertical Asymptote Lines
Vertical asymptote of natural log | Limits | Differential Calculus | Khan Academy
Комментарии
 0:29:04
0:29:04
 0:04:23
0:04:23
 0:07:07
0:07:07
 0:10:28
0:10:28
 0:10:54
0:10:54
 0:02:42
0:02:42
 0:08:23
0:08:23
 0:04:14
0:04:14
 0:11:16
0:11:16
 0:34:57
0:34:57
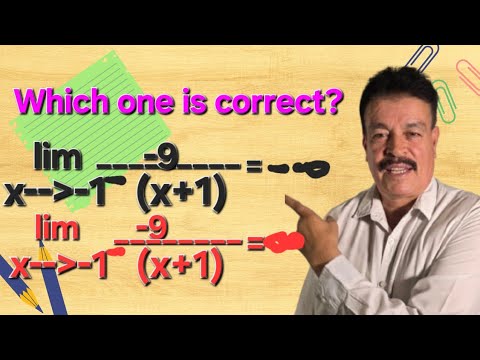 0:17:11
0:17:11
 0:00:36
0:00:36
 0:03:28
0:03:28
 0:02:44
0:02:44
 0:04:46
0:04:46
 0:01:46
0:01:46
 0:06:46
0:06:46
 0:02:16
0:02:16
 0:05:31
0:05:31
 0:19:24
0:19:24
 0:01:34
0:01:34
 0:06:59
0:06:59
 0:15:59
0:15:59
 0:07:00
0:07:00