filmov
tv
Math 201 Lecture 34 - Applications of definite integrals and integration by susbstitution

Показать описание
In this lecture, after learning about one of the most important pieces of information ever in the last lecture (the Fundamental Theorem of Calculus), we go into some applications of definite integrals.
Some followed directly from the fundamental theorem, like finding areas under curves. Others were more subtle, like using a definite integral to find the average value of a function on some interval, or finding an x-value in that interval such that the function takes on the average value. We also look at an example we've talked about a lot: a position-velocity problem, where we used definite integrals to find the total distance traveled by an object, or its displacement from some initial position.
We also looked at an integral technique: integration by substitution. One of the simplest integration techniques out there, and we can use it to integrate certain non-trivial integrals (integrals that, at first glance, do not appear to conform to a rule that we can apply--but do after a substitution transformation). The technique is explained with examples, and the conditions necessary to make the technique work are discussed.
Some followed directly from the fundamental theorem, like finding areas under curves. Others were more subtle, like using a definite integral to find the average value of a function on some interval, or finding an x-value in that interval such that the function takes on the average value. We also look at an example we've talked about a lot: a position-velocity problem, where we used definite integrals to find the total distance traveled by an object, or its displacement from some initial position.
We also looked at an integral technique: integration by substitution. One of the simplest integration techniques out there, and we can use it to integrate certain non-trivial integrals (integrals that, at first glance, do not appear to conform to a rule that we can apply--but do after a substitution transformation). The technique is explained with examples, and the conditions necessary to make the technique work are discussed.
 1:09:28
1:09:28
 0:49:03
0:49:03
 0:20:25
0:20:25
 0:19:57
0:19:57
 0:34:50
0:34:50
 0:12:49
0:12:49
 0:32:02
0:32:02
 1:06:36
1:06:36
 0:12:36
0:12:36
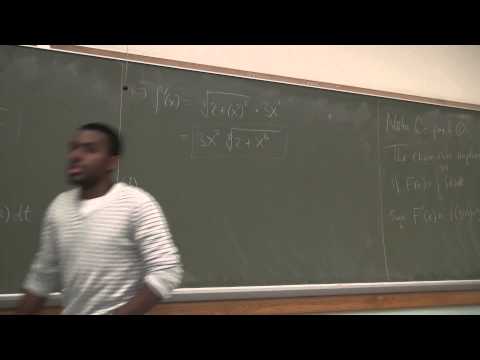 1:02:24
1:02:24
 0:23:42
0:23:42
 0:20:33
0:20:33
 0:27:30
0:27:30
 0:19:40
0:19:40
 0:21:06
0:21:06
 1:00:35
1:00:35
 0:19:47
0:19:47
 0:08:14
0:08:14
 0:13:57
0:13:57
 1:06:36
1:06:36
 0:28:36
0:28:36
 0:12:44
0:12:44
 0:23:37
0:23:37
 0:56:49
0:56:49