filmov
tv
Rethinking the real line #SoME3

Показать описание
We take a geometric approach to rational numbers, to rethink how to organize the real line. Along the way, we visualize Diophantine approximation and continued fractions. And your favourite number, pi.
Much of the mathematics here is based on the following article:
A big thanks to the Summer of Math Exposition competition for the motivation to make this happen, and a big thanks to my audience for forgiving my video-editing non-skills.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Music used in the video:
Walk Through the Park -- TrackTribe
George Street Shuffle -- Kevin MacLeod
Quarter Mix -- Freedom Trail Studio
Love Struck -- E's Jammy Jams
Much of the mathematics here is based on the following article:
A big thanks to the Summer of Math Exposition competition for the motivation to make this happen, and a big thanks to my audience for forgiving my video-editing non-skills.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Music used in the video:
Walk Through the Park -- TrackTribe
George Street Shuffle -- Kevin MacLeod
Quarter Mix -- Freedom Trail Studio
Love Struck -- E's Jammy Jams
Rethinking the real line #SoME3
25 Math explainers you may enjoy | SoME3 results
The Secret Bond between the Naturals and the Reals #SoME3
Unsolved Math: The No-Three-In-Line Problem #SOME3
Rethinking Functional Limits (#SoME3 submission)
The two points that lie on every circle (???) #SoME3
Counting in Imaginary (featuring Irrationals) #SoME3
Irrationality of Imperfect Squares #math #some3 #irrationalnumber
The First Real Application of Category Theory #SoME3
Integration — Two Ways to Visualize #some3
This Function Maps Any Interval to the Real Line (Conway's Base-13 Function)
How subtraction makes the universe more robust | #SoME3
What Happens If We Add Fractions Incorrectly? #SoME3
Just some cool fractals | #SoME3 #shorts
The Mathematics of Mechanisms (#SoME3)
The Math of Bubbles // Minimal Surfaces & the Calculus of Variations #SoME3
The Verhoeff-Gumm Check Digit Algorithm #SoME3
THINGS THAT EVERY QR CODE HAVE #some3
The Art of Procedural Noise #SoME3
Is the Logistic Map hiding in the Mandelbrot Set? | #SoME3
Responsive Design — Perfecting my #SoME3 paper
Not Enough Volunteers, Math Explains Why? #SoME3
The math of saving the Enola Gay #SoME3
Rotation + Translation = Rotation. Animated proof | #SoME3
Комментарии
 0:14:54
0:14:54
 0:22:12
0:22:12
 0:12:01
0:12:01
 0:12:52
0:12:52
 0:17:43
0:17:43
 0:32:22
0:32:22
 0:37:39
0:37:39
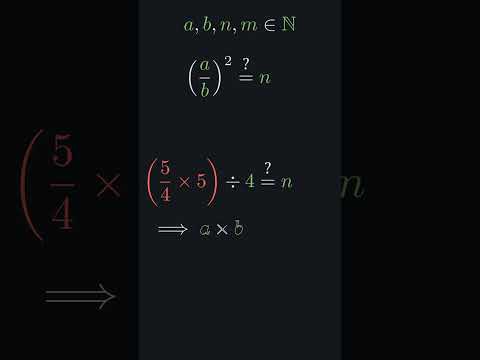 0:00:59
0:00:59
 0:12:45
0:12:45
 0:00:48
0:00:48
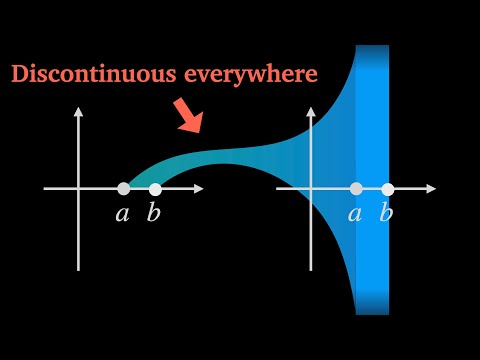 0:09:03
0:09:03
 0:18:23
0:18:23
 0:29:04
0:29:04
 0:00:59
0:00:59
 0:13:45
0:13:45
 0:17:27
0:17:27
 0:17:00
0:17:00
 0:00:43
0:00:43
 0:32:03
0:32:03
 0:12:14
0:12:14
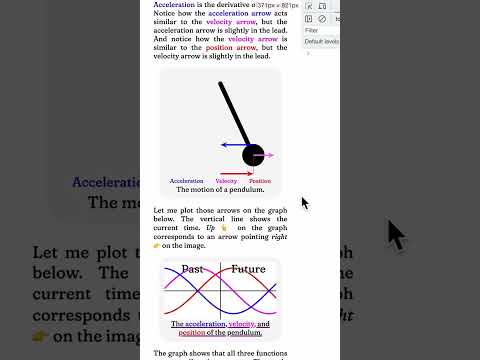 0:00:48
0:00:48
 0:04:04
0:04:04
 0:25:53
0:25:53
 0:10:56
0:10:56