filmov
tv
Solving sin(alpha+beta)=sin(alpha)+sin(beta)

Показать описание
If you need to post a picture of your solution or idea:
#TrigonometryProblems #TrigonometricEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
#TrigonometryProblems #TrigonometricEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
Solving sin(alpha+beta)=sin(alpha)+sin(beta)
How to find sin(alpha + beta) when given sin(alpha) and cos(beta)
sin(alpha + beta) + sin(alpha - Beta) = 2sinacosB
✅ ✅ Have you seen this Sin(Alpha + Beta) Visualization?? ✔️👀
AMBQID134 | Question with Solution | Trigonometry | Sin Alpha Cos Alpha Sin Beta Cos Beta | AMBPi49
Prove by vector methods that `sin(alpha+beta)=sin alphacos beta+cos alphasin beta`
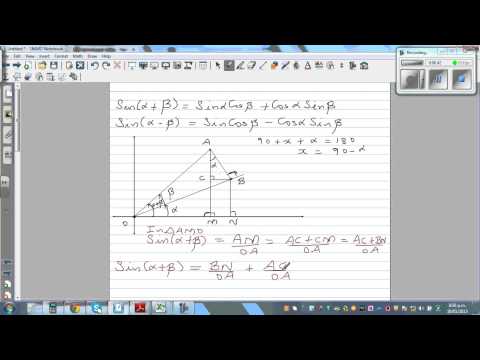
Proof of formula Sin(α+β)=SinαCosβ+CosαSinβ and Sin(α-β)=SinαCosβ-CosαSinβ
`(sin(alpha+beta))(sin(alpha-beta))=(a+b)(a-b)` then `(tan alpha)(tan | Class 12 Maths | Doubtnut
If `sin(alpha+beta) = 1` and `sin(alpha-beta) =1/2` where `0 lt=alpha,beta lt= pi/2` then find...
To Prove Cos(α-β), Sin(α-β), Cos(α+β), Sin(α+β) formulas using Vector Method
When mathematicians get bored (ep1)
If `alpha+beta-gamma=pi` and `sin^2alpha+sin^2beta-sin^2gamma=lambda sinalpha sinbeta cosgamma
Solve | sin 30 degree | using calculator (Casio fx-991MS)
If alpha + beta = pi/2 prove that (cos alpha + i * sin alpha)(cos beta + i * sin beta) = i
Find cos(α-β) given sin(α) and sin(β) and quadrants
if cos alpha + beta =0, then sin alpha-beta is#shorts #exemplar #class10 MCQ#trigonometry
Let `cos(alpha+beta)=(4)/(5)` and let `sin(alpha-beta)=(5)/(13)`, where `0 le alpha`, `beta=(p
sin alpha and sin beta are the solution of a cos theta + b sin theta=c The value of sinalpha sinbeta
IIT Bombay CSE 😍 #shorts #iit #iitbombay
MULTIPLE & SUBMULTIPLE ANGLES PART 11
Relation b/w Trigonometrical functions | sin cos tan cot sec | #short | #shorts | #trigonometry
🤣Modi ji ne to math ki esi taisi kar diye🤣🙆🏻♂️ #shorts #youtubeshorts #viral
`(sinalpha+sinbeta-sin(alpha+beta))/(sinalpha+sinbeta+sin(alpha+beta))=tan(alpha/2)tan(beta/2)`
If sin(alpha + beta) / sin(alpha - beta) = a + b / a - b then a tan beta = b tan alpha @EAG
Комментарии
 0:09:28
0:09:28
 0:01:59
0:01:59
 0:01:16
0:01:16
 0:00:51
0:00:51
 0:03:55
0:03:55
 0:04:01
0:04:01
 0:14:40
0:14:40
 0:05:50
0:05:50
 0:04:41
0:04:41
 0:20:24
0:20:24
 0:00:37
0:00:37
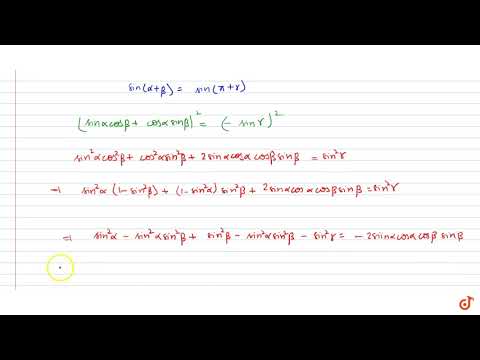 0:03:57
0:03:57
 0:00:24
0:00:24
 0:02:26
0:02:26
 0:13:46
0:13:46
 0:00:49
0:00:49
 0:03:27
0:03:27
 0:03:09
0:03:09
 0:00:11
0:00:11
 0:11:07
0:11:07
 0:00:24
0:00:24
 0:00:24
0:00:24
 0:03:49
0:03:49
 0:05:22
0:05:22