filmov
tv
A Curious Derivative of an Infinite Sine Power Tower Tetration... - Papa's Improvised Session #10
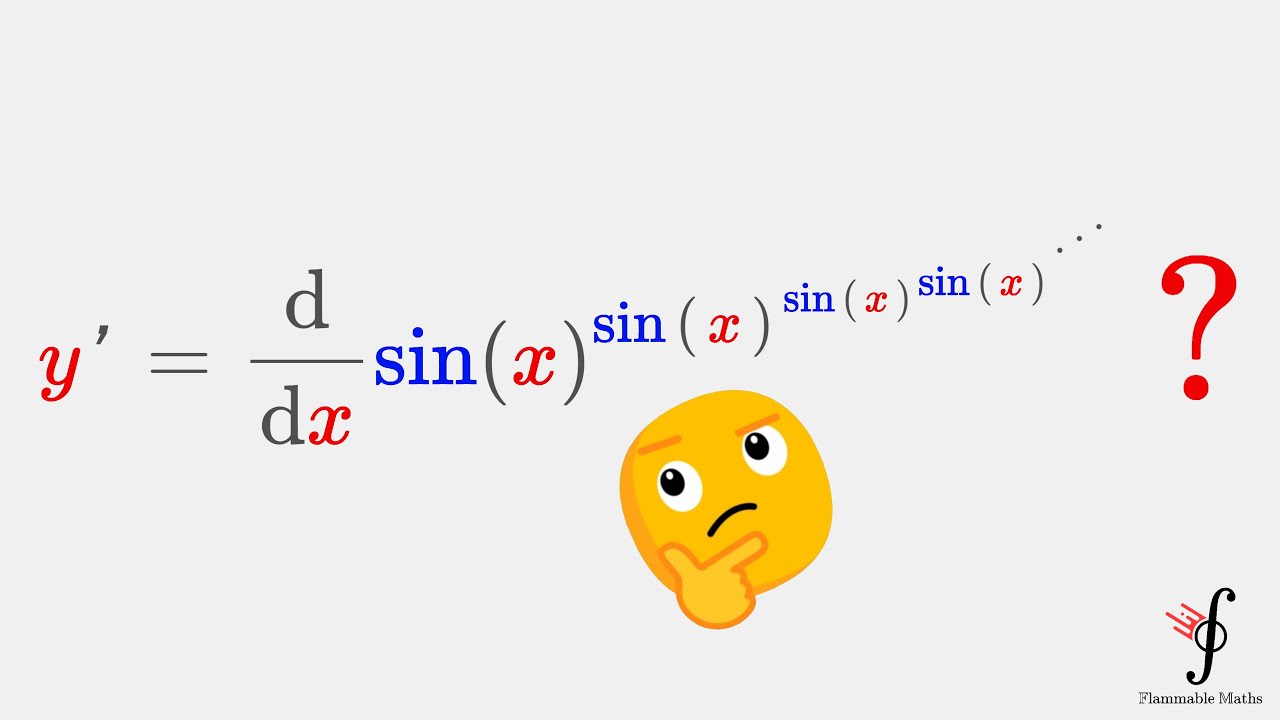
Показать описание
Today we differentiate the infinite tetration of sin(x) wrt x :) Enjoy! =D
This video has been sponsored by Wondershare btw :)
Help me create more free content! =)
--------------------------------------------------------------------------------
Wanna send me some stuff? lel:
Postfach 11 15
06731 Bitterfeld-Wolfen
Saxony-Anhalt
Germany
--------------------------------------------------------------------------------
A Curious Derivative of an Infinite Sine Power Tower Tetration... - Papa's Improvised Session #...
9.35 | Differentiation | Derivative of an Implicit Function
9.42 | Differentiation | Derivative of an Implicit Function
9.6 | Differentiation | Derivative of an Implicit Function
9.44 | Differentiation | Derivative of an Implicit Function
Maths Curious Series - Why is derivative of natural log 1/x?
9.38 | Differentiation | Derivative of an Implicit Function
How to Find the Derivative Using Power Rule | #APCalculus
CSIR NET Numerical Analysis|GATE Numerical Method|Newton Divided DifferenceNumerical Differentiation
Here are simple mnemonics toremember these 5 common derivatives.
the complex derivative is strange...
Unveiling Derivatives Angel or Devil #trending #finance #financeshorts
What is a Derivative? | Calculus for 1st Graders - Part 5
Unveiling Derivatives: Exploring Function Derivation Step by Step
How to take the Derivative | Derivatives for Beginners - #shorts #shortvideo #maths #mathematics
Calculus 1 CH 3 Derivatives (22 of 24) A Strange Example
Curiosity Corner Episode 2: DERIVATIVES OF STANDARD FUNCTIONS
Implicit Differentiation Say Wha?
Derivatives explained in 60s #Derivatives #Calculus #MathExplained #Speedometer #MathInRealLife
What is a Derivative?
🚀 Fast Derivative Solutions! 🧮#MathTricks #youtubeshort #ytshorts
🚀 Fast Derivative Solutions! 🧮#MathTricks #youtubeshort #ytshorts
Derivative Formula
Beyond Limits: How Infinitesimals Solve the Derivative of x^2 #shorts
Комментарии
 0:11:06
0:11:06
 0:07:32
0:07:32
 0:02:14
0:02:14
 0:01:28
0:01:28
 0:15:48
0:15:48
 0:01:01
0:01:01
 0:03:59
0:03:59
 0:07:50
0:07:50
 1:43:53
1:43:53
 0:00:45
0:00:45
 0:26:37
0:26:37
 0:00:31
0:00:31
 0:00:39
0:00:39
 0:00:46
0:00:46
 0:00:21
0:00:21
 0:02:35
0:02:35
 0:04:20
0:04:20
 0:00:34
0:00:34
 0:00:56
0:00:56
 0:00:53
0:00:53
 0:00:41
0:00:41
 0:00:40
0:00:40
 0:00:06
0:00:06
 0:00:37
0:00:37