filmov
tv
How to Differentiate ln(sqrt(x)) By Rewriting and using the Power Rule for Logarithms
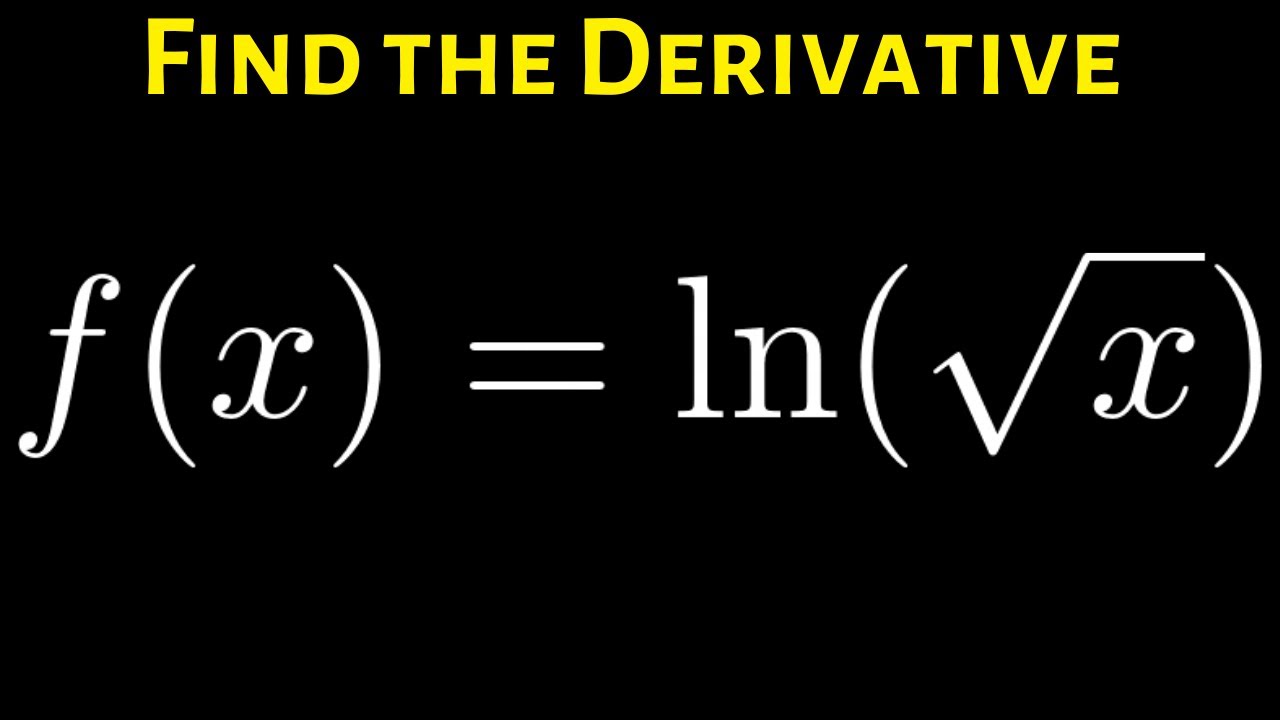
Показать описание
How to Differentiate ln(sqrt(x)) By Rewriting and using the Power Rule for Logarithms
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus Integration Insanity
Differential Equations Course
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
#mathsorcerer #onlinemathhelp
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus Integration Insanity
Differential Equations Course
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
#mathsorcerer #onlinemathhelp
How to Differentiate ln(sqrt(x)) By Rewriting and using the Power Rule for Logarithms
Derivative of ln(sqrt(x+1)) ❖ Calculus
How to Find the Derivative of the Square Root of the Natural Log of x: sqrt(ln(x))
Differentiate h(x) = ln(x+ sqrt(x^2+1)). Natural logarithms
Derivative of ln(sqrt(x)) #shorts #calculus
First and Second Derivative of sqrt x ln x
derivative of ln(x+sqrt(x^2-1)), calculus 1 tutorial
Calculus Natural Log Derivatives ln (2x+1)^3/sqrt(x^2 + 1)
How to find the derivative of ln(sqrt(x^2+1)) using the chain rule and log properties.
Using power rule with square root to take derivative on a logarithm
f(x) = sqrt(x) * ln x, Differentiate the function
Derivative of sqrt(lnx) with Chain Rule | Calculus 1 Exercises
77 Derivative of ln(sqrt(x^2- 1))
Differentiate f(x)= sqrt(x) ln x. And f(x) = x ln x - x. Natural logarithms
Differentiate g(x) = ln(x sqrt(x^2-1)). Natural logarithms
Derivative of f(x) = ln(x + sqrt(2 + x^2)) with the Chain Rule
Differentiate the function.h(x) = ln(x + sqrt(x^(2) − 3))
Derivative of f(x) = sqrt(ln(x))
G(u) = ln sqrt((3u + 2)/(3u - 2)), Differentiate the function
Differentiate H(z)= ln sqrt((a^2-z^2)/(a^2+z^2)). Natural logarithms
Solve ln(sqrt(x + 4)) = 1 #shorts
How to differentiate ln(sqrt(2+cos^2x))
integral of ln(sqrt(x+1)+sqrt(x)) by trig sub
Find the limit as x approaches infinity for (ln sqrt(x))/x^2. l’Hospitals’ Rule
Комментарии
 0:01:53
0:01:53
 0:03:58
0:03:58
 0:02:55
0:02:55
 0:04:05
0:04:05
 0:00:55
0:00:55
 0:04:48
0:04:48
 0:03:40
0:03:40
 0:02:15
0:02:15
 0:03:10
0:03:10
 0:02:20
0:02:20
 0:01:30
0:01:30
 0:02:17
0:02:17
 0:01:33
0:01:33
 0:03:42
0:03:42
 0:02:53
0:02:53
 0:02:55
0:02:55
 0:02:42
0:02:42
 0:01:20
0:01:20
 0:00:52
0:00:52
 0:05:57
0:05:57
 0:00:36
0:00:36
 0:03:57
0:03:57
 0:10:13
0:10:13
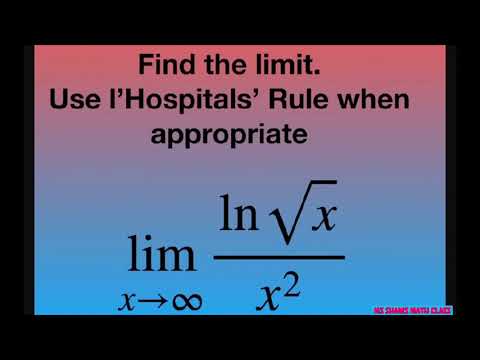 0:02:41
0:02:41