Multiple Regression in Excel - P-Value; R-Square; Beta Weight; ANOVA table (Part 2 of 3)

Check out our new Data Analysis in Excel text:

This video illustrates how to perform a multiple regression statistical analysis in Microsoft Excel using the Data Analysis Toolpak.

Multiple Regression in Excel

Multiple Regression
Regression
R-Squared
ANOVA table
Regression Weight
Beta Weight
Predicted Value

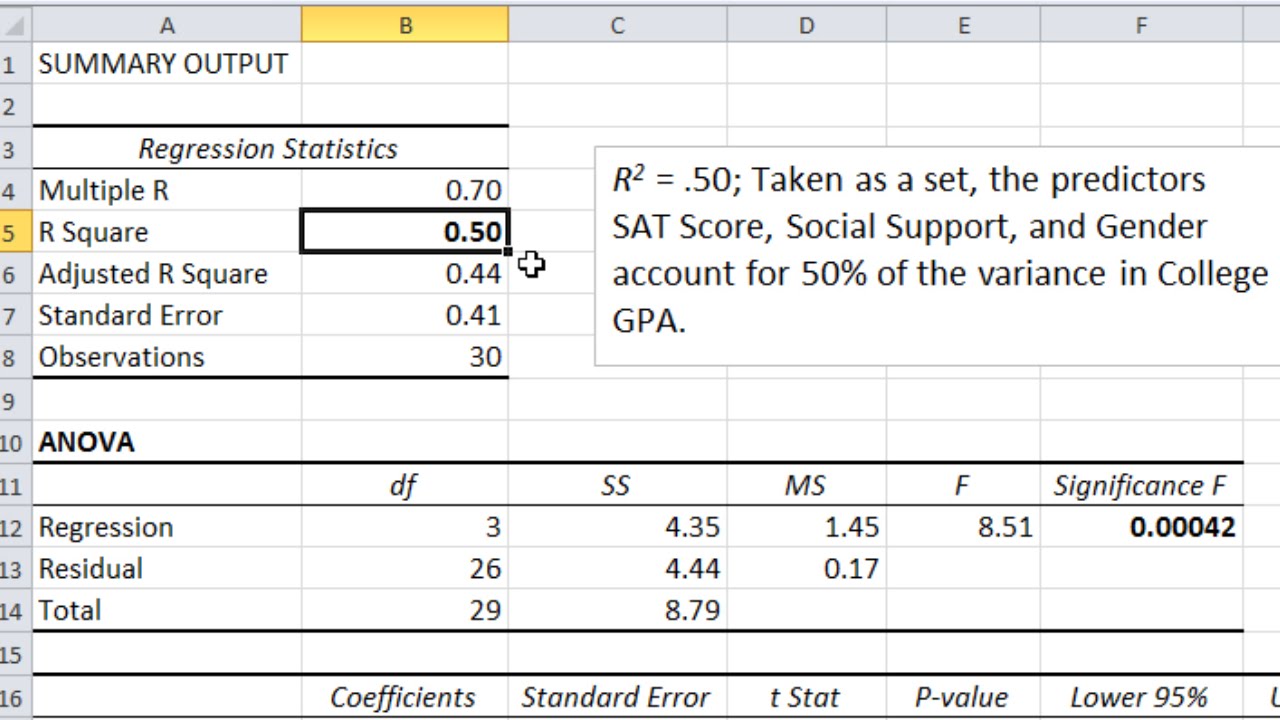
Video Transcript: and then I also want to go ahead and dial down these decimals. Let's do it to two decimal places. And then we'll go back and increase our p-values just a bit. So dial that down to two, that looks good. And then for my p value, which is significance F under ANOVA, and then the p-values here, let's go to increase these a bit more. So if we're comparing them to any other results, from any other analyses, SPSS or what-have-you, we can go ahead and make sure that they match up. OK that looks good. So I'll go ahead and shrink these just a bit more. Alright, so in multiple regression, there's two things that we're dealing with. We're dealing with the overall fit of what's called our model, and our model is where we use our three predictors to try and predict first-year college GPA. So that's our model, our whole, all of our values, that constitutes our model. And we're trying to assess how well the model fits overall, how well of a job did the three predictors help us predict college GPA overall, and then we also want to know how did the individual predictors do. So we're looking at two things, we're looking at the overall usefulness of the model, and then the usefulness of the individual predictors SAT score, social support, and gender. So we'll get started first with the overall fit. And that really concerns this first table of output, as well as the second table output. So let's start here. And in this video, we're just going to highlight some of the key features of multiple regression. In other videos we'll be diving in in more detail into some of these other aspects, such as the ANOVA tables, where these values come from, and so forth. So what we want to do in this video, focusing on the key values, we're going to be looking at R-square, we're going to be looking at the significance F, or the p-value under the ANOVA results, and we're also going to be looking at the p-values under, I'll call this coefficients here, for these three values, for our 3 predictors. OK so I put in boldface type the key values that we're interested in in this video. And the first is R-squared. R-squared indicates how well our three predictors, SAT score, social support, and gender, did as a set in predicting college GPA. Did they do a good job, did they do a bad job and so on. That's what R-squared is a measure of. And R-square ranges from 0 to 1. And the way we would interpret it, first of all, in this example, R-square is equal to .50, and we could interpret it as follows: taken as a set, the predictors SAT score, social support, and gender, account for 50% of the variance in college GPA. So in other words when we have an R-square what we do is we convert this to a percentage, in terms of interpretation, and that indicates the amount of variance in the dependent variable that was accounted for by the set of the independent variables. So since our decimal is .50, we convert that to a percent. That tells us that our predictors, SAT score, social support, and gender, collectively as a group, accounted for 50% of the variance in college GPA. Now it's important to note here that this doesn't mean that each of these three predictors accounted for one-third, exactly, of the 50% as there are three of them. So approximately SAT score accounted for 17%, social support accounted for 17%, and gender accounted for 17%. It does not mean that whatsoever. All it means is that when all three of those predictors are entered into this analysis or into this model, we can call it, as a group, they account for fifty percent of the variance in college GPA. Now it may be that SAT score accounts for 45% of the 50, we don't know yet at this point. All we know is a group, they account for 50%. How much variance we account for really depends on the discipline that one is working in. It can vary quite a bit. In the social sciences accounting for 50, 60, or 70% of the variance, in most applications, is pretty good. But in other areas, biology, chemistry, you may expect R-Square of .99 if you expect some process to be replicated almost identically. So it really depends on what you're working in, what area. But in the work I do, 50% would be considered pretty good we're working with predicting behavior in people. OK, next we have the ANOVA table. So the ANOVA table tells us whether or not this R-squared is significantly greater than 0. So the ANOVA table is testing, overall, the three predictors, SAT score, social support, and gender, do they predict college GPA significantly.

Subscribe today!