filmov
tv
Proof: The Product Rule of Differentiation

Показать описание
This video explains the proof of the product rule using the limit definition of the derivative.
Product rule proof | Taking derivatives | Differential Calculus | Khan Academy
Proof of The Product Rule
Proof: The Product Rule of Differentiation
Proof of the Product Rule from Calculus
Proving Product Rule
Visualizing the chain rule and product rule | Chapter 4, Essence of calculus
Product Rule Proof
Calculus 3.07f - Proof of the Product Rule
Vector algebra | proof of cosine Formulae | proof of prejection formulae | bsc | gate physics
Proof of the product rule
COOL Product Rule Proof
a neat product rule proof
PROOF of Product Rule of Differentiation
Product Rule - Intuitive Proof
Derivative Rules - Proof of the Product Rule
Proof of Product Rule in Differentiation
a unifying product quotient rule proof
Product Rule | Differencial Calculus
The Product Rule - A Proof That's Simple, Clever, and Fun - Simply Put
How to derive the PRODUCT RULE from scratch
Proving the power, product and quotient rules by using logarithmic differentiation & the chain r...
Log Product Rule Proof
Calculus Proofs: the Product Rule
Differentiation - proving the product rule from the chain rule
Комментарии
 0:09:25
0:09:25
 0:15:35
0:15:35
 0:04:46
0:04:46
 0:06:07
0:06:07
 0:14:44
0:14:44
 0:15:56
0:15:56
 0:04:32
0:04:32
 0:09:53
0:09:53
 1:11:16
1:11:16
 0:09:00
0:09:00
 0:06:09
0:06:09
 0:02:20
0:02:20
 0:07:56
0:07:56
 0:09:09
0:09:09
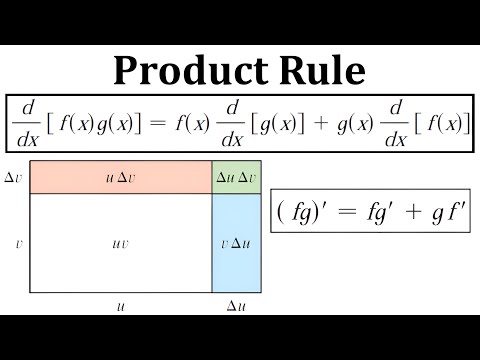 0:11:42
0:11:42
 0:05:24
0:05:24
 0:03:22
0:03:22
 0:09:26
0:09:26
 0:05:43
0:05:43
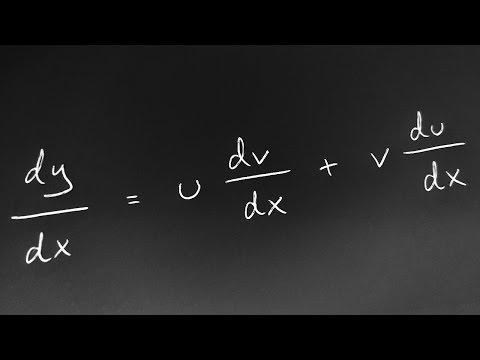 0:03:39
0:03:39
 0:17:55
0:17:55
 0:01:58
0:01:58
 0:09:19
0:09:19
 0:03:54
0:03:54