filmov
tv
Mathematical Coincidences
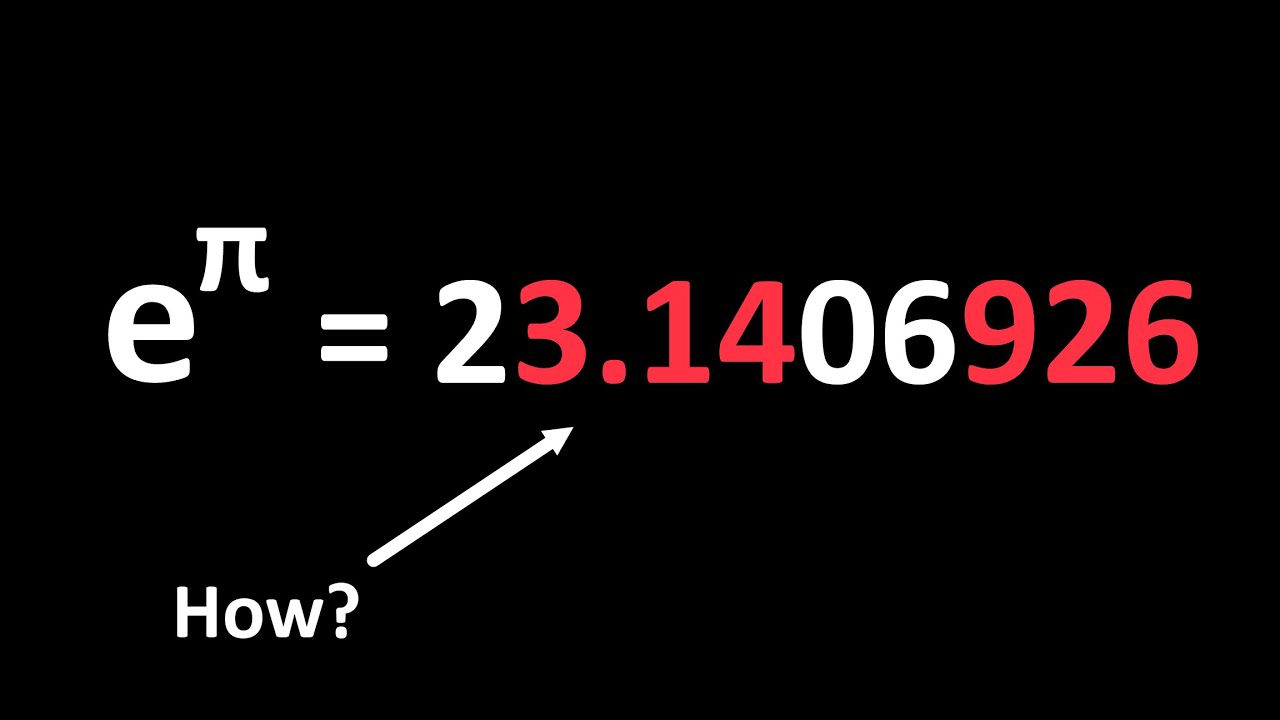
Показать описание
In this video we take a look at some fun mathematical coincidences!
#math
#weird
#coincidence
#funfacts
#math
#weird
#coincidence
#funfacts
Mathematical Coincidences
'It's just a Coincidence'
The most dangerous problem in math
The Simplest Math Problem No One Can Solve - Collatz Conjecture
A Math Fact for the New Year 2025!
Strange Coincidences in Math 😂 #Shorts #math #maths #mathematics #strange
How a mathematician dissects a coincidence
An amazing mathematical coincidence
Strange Coincidences in Math 😂 #Shorts #math #maths #mathematics #strange
Coincidence in mathematics #mathstricks
Math Magic
The Oldest Unsolved Problem in Math
15 Mind Blowing Math Facts | Insane but True
AMAZING number patterns in the Bible!
Littlewoods law! #miracle #explained #coincidence #learning #math #probability #learneclecticthings
4 𝙢𝙞𝙣𝙪𝙩𝙚𝙨 𝙤𝙛 𝙄𝙉𝙏𝙀𝙍𝙀𝙎𝙏𝙄𝙉𝙂 𝙈𝘼𝙏𝙃...
The Mathematics of Coincidence - Sarah Hart
Coincidence in mathematics
😳 Coincidence in Math
150/365 3 Coincidences That Are Hard To Digest #coincidences #365daysofmath
Attempt to get mathematical coincidences for Fermat primes and primes in Brocard’s conjecture
Coincidence
Cube Roots Math Fun - Coincidence or nah..?
37 huh?
Комментарии
 0:08:11
0:08:11
 0:08:28
0:08:28
 0:01:00
0:01:00
 0:22:09
0:22:09
 0:00:58
0:00:58
 0:00:14
0:00:14
 0:06:14
0:06:14
 0:03:39
0:03:39
 0:00:17
0:00:17
 0:00:16
0:00:16
 0:19:31
0:19:31
 0:31:33
0:31:33
 0:22:32
0:22:32
 0:05:39
0:05:39
 0:00:46
0:00:46
 0:04:35
0:04:35
 0:58:26
0:58:26
 0:00:14
0:00:14
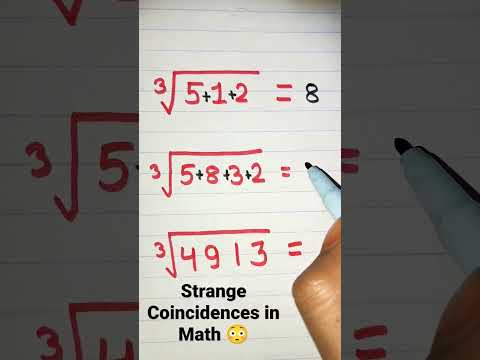 0:00:14
0:00:14
 0:00:51
0:00:51
 0:04:41
0:04:41
 0:00:48
0:00:48
 0:00:18
0:00:18
 0:00:59
0:00:59