filmov
tv
Calculus 3: Green's Theorem (10 of 21) With a Conservative Vector Field: Ex. 2

Показать описание
In this video I will find the work done in a conservative vector field by integrating along the path x^2+y^2= a^2. Ex. 2
Next video in the series can be seen at:
Calculus 3: Green's Theorem (10 of 21) With a Conservative Vector Field: Ex. 2
Calculus 3: Green's Theorem (21 of 21) More Examples 4
Green's Theorem, explained visually
Green's theorem example 1 | Multivariable Calculus | Khan Academy
Calculus 3: Green's Theorem (18 of 21) Using Green's Theorem to Find Area
Calc 3: Green's Theorem (Step by Step)
Green's Theorem
||Green's Theorem|| Calculus|| by Howard Anton||10th Edition|| Exercise 15.4|| Question no.3||
Vector integration Green's theorem best & easy example(PART-1)
Calc 3: Green's Theorem (TI-nSpire CX CAS)
Calculus 3: Green's Theorem (8 of 21) Graphical Representation of a Vector Field
Green's Theorem in Simple Way | Vector Calculus | Mathematics 2 New Syllabus | Maths 2 GTU
Green's Theorem #calculus #vectorcalculus
Calculus 3: Green's Theorem (11 of 21) With a NON-Conservative Vector Field: Ex. 2
|| Vector Calculus || Lecture-10 || Green's Theorem || Dr Sonendra Gupta ||
Calculus 3: Green's Theorem (9 of 21) A Conceptual Look
Calc 3: Green's Theorem (Solved by Hand)
Calculus 3: Green's Theorem (13 of 21) With a NON-Conservative Vector Field: Ex. 3 (Line Integr...
Multivariable Calculus - Using Green’s Theorem
Green's Theorem Example | Calculus 3 | Vector Calculus
Calculus 3: Green's Theorem (6 of 21) With a Conservative Vector Field
Calculus 3, Session 34 -- Green's Theorem
Divergence, Flux, and Green's Theorem // Vector Calculus
Green's Theorem|| Calculus|| by Howard Anton||10th Edition|| Exercise #15.4|| Question no.1||
Комментарии
 0:08:54
0:08:54
 0:05:14
0:05:14
 0:06:32
0:06:32
 0:10:31
0:10:31
 0:03:57
0:03:57
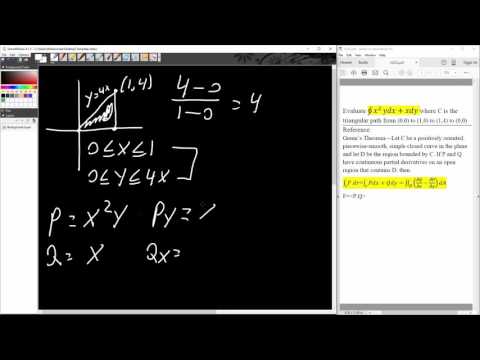 0:03:02
0:03:02
 0:06:42
0:06:42
 0:05:40
0:05:40
 0:14:16
0:14:16
 0:02:54
0:02:54
 0:07:18
0:07:18
 0:08:47
0:08:47
 0:01:00
0:01:00
 0:05:34
0:05:34
 0:15:16
0:15:16
 0:04:19
0:04:19
 0:01:56
0:01:56
 0:07:07
0:07:07
 0:10:31
0:10:31
 0:02:45
0:02:45
 0:02:31
0:02:31
 1:06:19
1:06:19
 0:10:33
0:10:33
 0:13:17
0:13:17