filmov
tv
Gaussian Quadrature 3: The Explanation of the Technique

Показать описание
Gaussian Quadrature 3: The Explanation of the Technique
Gaussian Quadrature | Lecture 40 | Numerical Methods for Engineers
Preview: The Magic of Gaussian Quadrature - A Billion Times Better than the Next Best Thing
Gaussian Quadrature - Analysis
An introduction to numerical integration through Gaussian quadrature
Numerical Analysis: Gaussian Quadrature
A brief introduction to Gauss quadrature
Advantage of using Gaussian quadrature
Gaussian Quadrature
Numerical Integration - Gaussian Quadrature
Gaussian Quadrature
Gaussian quadrature
Gaussian Quadrature - Motivation and Example
Quick Revision of Gauss Quadrature Formula| Direct Example| One point|Two Point| Three Point Formula
Gauss-Legendre Quadrature 3: The proof
why gauss quadrature is best for integration ?
Numerical Analysis - Gauss Quadrature Rule for Integration (#1)
Week 10 : Lecture 51 : Numerical Integration: Gaussian Quadrature Rule
Gaussian Quadrature
Numerical Analysis - Gauss Quadrature Rule for Integration (#2)
Gaussian quadrature formula for three points
Gauss Quadrature Example
Numerical Integration : Introduction to Gauss Quadrature
Numerical Integration - Gaussian Quadrature with example
Комментарии
 0:12:38
0:12:38
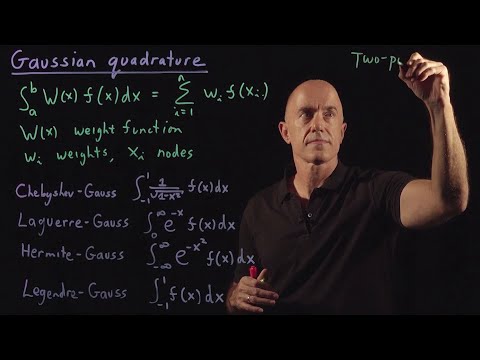 0:08:51
0:08:51
 0:09:35
0:09:35
 0:18:41
0:18:41
 0:26:04
0:26:04
 0:36:20
0:36:20
 0:11:13
0:11:13
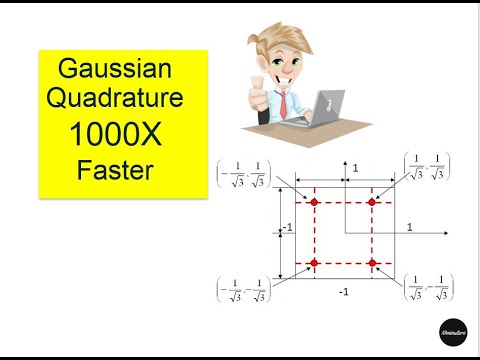 0:06:36
0:06:36
 0:20:49
0:20:49
 0:17:17
0:17:17
 0:48:29
0:48:29
 0:10:42
0:10:42
 0:13:29
0:13:29
 0:04:05
0:04:05
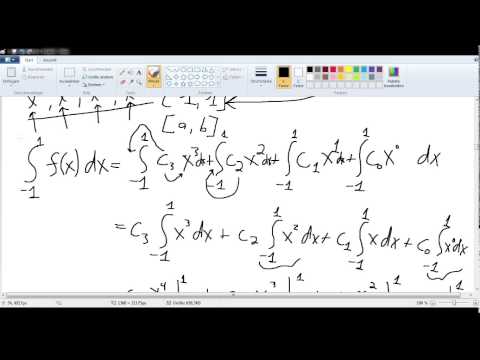 0:10:45
0:10:45
 0:01:06
0:01:06
 0:01:39
0:01:39
 0:29:24
0:29:24
 0:55:47
0:55:47
 0:06:58
0:06:58
 0:21:25
0:21:25
 0:19:36
0:19:36
 0:06:47
0:06:47
 0:09:19
0:09:19