filmov
tv
ENSPM2021 | 16julho | Peter Scholze
Показать описание
Condensed Mathematics
Abstract: (joint with Dustin Clausen) It is a well-known problem that topological spaces have no good categorical properties — for example, topological abelian groups do not form an abelian category, and in a complex of topological vector spaces, differentials may not have closed image, leading to pathological cohomology groups. However, we realized that one can replace topological spaces by the closely related notion of condensed sets, resolving all of these foundational problems. This makes it possible to develop new foundations for both nonarchimedean and archimedean functional analysis, even allowing a very general formalism of analytic spaces — encompassing complex manifolds, real manifolds of all flavours, schemes, formal schemes, rigid-analytic varieties, and adic spaces into one unified framework. We will try to give an overview of these ideas.
Abstract: (joint with Dustin Clausen) It is a well-known problem that topological spaces have no good categorical properties — for example, topological abelian groups do not form an abelian category, and in a complex of topological vector spaces, differentials may not have closed image, leading to pathological cohomology groups. However, we realized that one can replace topological spaces by the closely related notion of condensed sets, resolving all of these foundational problems. This makes it possible to develop new foundations for both nonarchimedean and archimedean functional analysis, even allowing a very general formalism of analytic spaces — encompassing complex manifolds, real manifolds of all flavours, schemes, formal schemes, rigid-analytic varieties, and adic spaces into one unified framework. We will try to give an overview of these ideas.
0:59:34
ENSPM2021 | 16julho | Peter Scholze
0:00:06
collected work of Peter scholze
0:03:44
ICM: Peter Scholze
0:00:27
Why Didn’t Math Teachers Teach This
1:03:05
Peter Scholze: The pro-etale site
0:53:31
Perfectoid spaces (Peter Scholze) AWS 2017 Closing
0:16:05
Deutschlands jüngste Mathe-Professorin Lisa Hartung: Talk am Gonsbach in Mainz
0:00:46
Live stream this Friday
0:01:00
Happy Birthday Gerd Faltings || Fields Medalist || Algebraic Geometry ||
1:10:55
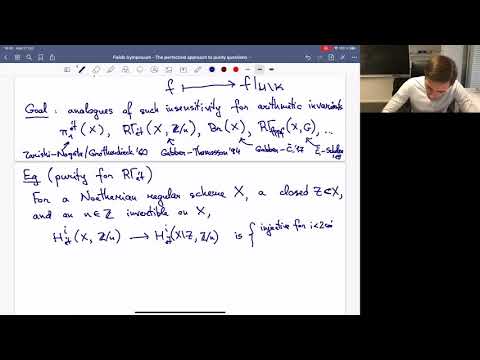
The perfectoid approach to purity questions
1:03:29
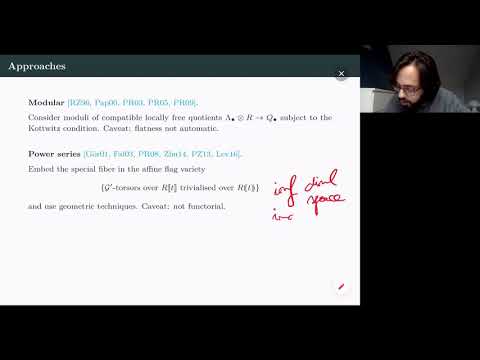
On the p-adic theory of local models
0:57:38
Peter Scholze - Liquid vector spaces
1:02:19
Dustin Clausen - Toposes generated by compact projectives, and the example of condensed sets
1:17:04
Johan Commelin, The Liquid Tensor Experiment
1:06:11
Geometrization of the local Langlands correspondence
0:31:15
Peter Schultz: Playing with the Molecules of Life
0:51:51
Finiteness properties of p-adic etale cohomology of the Drinfeld tower
0:02:01
This house owns itself – no1s1
2:01:46
Dynamic Neural Fields: Numerical Simulations and Applications to Robotics
0:25:53
Towards an algebraic independence result for certain p -adic series.
1:04:56
Session 8: Masterclass in Condensed Mathematics
1:04:20
p-adic etale tate twists and syntomic cohomology
1:00:27
Session 15: Masterclass in Condensed Mathematics
0:31:54
Reuben Learns: Nikolaus-Scholze 'On Topological Cyclic Homology' 1
Комментарии