Tangent to a Hyperbola explained in a simple manner with an actual solved 2017 JEE Question

Tangent to a Hyperbola explained in a simple manner with an actual solved 2017 JEE Question. JEE Maths XI Hyperbola

EQUATION OF TANGENT:
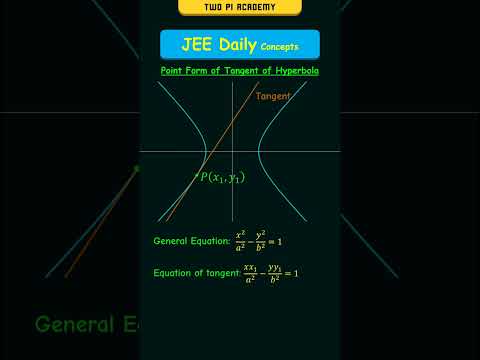
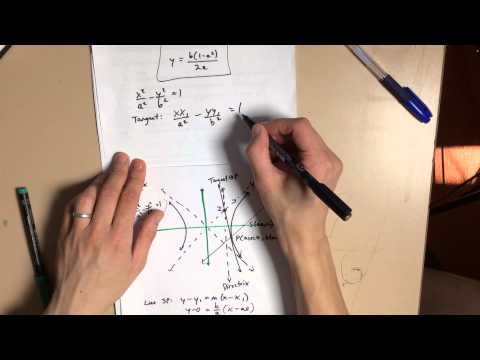
Point form: The equation of tangent to the hyperbola x^2/a^2 -y^2/b^2 =1 at (x1, y1) is (xx_1)/a^2 -(yy_1)/b^2 =1.
Proof: Differentiating w.r.t. x, we get dy/dx=(b^2 x)/(a^2 y)
Slope of the tangent at (x1, y1) is, m = (b^2 x_1)/(a^2 y_1 )
Equation of tangent at (x1, y1) is y __ y1 = (b^2 x_1)/(a^2 y_1 ) (x-x_1 )
⟹ a^2 yy_1-a^2 y_1^2=b^2 xx_1-b^2 x_1^2
⟹ b^2 xx_1-a^2 yy_1=b^2 x_1^2-a^2 y_1^2
⟹(xx_1)/a^2 -(yy_1)/b^2 =(x_1^2)/a^2 +(y_1^2)/b^2
⟹ (xx_1)/a^2 -(yy_1)/b^2 =1 (∵(x_1,y_1 ) lie on hyperbola (x_1^2)/a^2 +(y_1^2)/b^2 =1)
T = 0

Parametric Form: The equation of the tangent to the hyperbola x^2/a^2 -y^2/b^2 =1 at
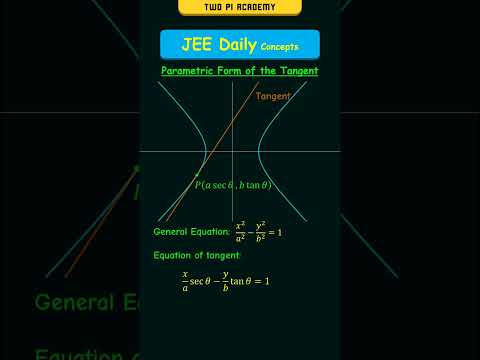
(a secθ , b tanθ) is x/a secθ-y/b tanθ=1.
Proof: Using the point form of the tangent equation, we get x(asecθ)/a^2 -y(btanθ)/b^2 =1
⟹x/a secθ-y/b tanθ=1
Note: The tangent at the point P (α) and Q (β) intersects at the point R = [(a cos⁡((α - β)/2))/cos⁡((α + β)/2) ,(b sin⁡((α + β)/2))/cos⁡((α + β)/2) ]
(III) Slope Form: The equations of the tangents of slope m to the hyperbola x^2/a^2 -y^2/b^2 =1 are
y = mx±√(a^2 m^2-b^2 )
Proof: Let the equation of tangent with slope m is y = mx + c........ (1)
Let (x1, y1) be the point of contact.
⟹ Tangent at (x1, y1) on the hyperbola is (xx_1)/a^2 -(yy_1)/b^2 =1 ....... (2)
Equations (1) and (2) represent the same ⟹(x_1/a)/m=(- y_1/b^2 )/(-1)=-1/c ⇒x_1=-(a^2 m)/c & y_1=-b^2/c
Since (x1, y1) lie on y = mx + c also, we get y1 = mx1 + c ⇒ -b^2/c=(a^2 m^2)/c+c ⇒ c2 = a2m2 – b2
c = ± √(a^2 m^2-b^2 )
The equations of the tangents in slope form are y = mx± √(a^2 m^2-b^2 ) and the points of contact are (± a^2/√(a^2 m^2 - b^2 )± b^2/√(a^2 m^2 - b^2 ))