What is the Cartesian Product of Graphs? (Discrete Math) +3 examples!

This video will explain what a cartesian product in graph theory is and how to calculate it.

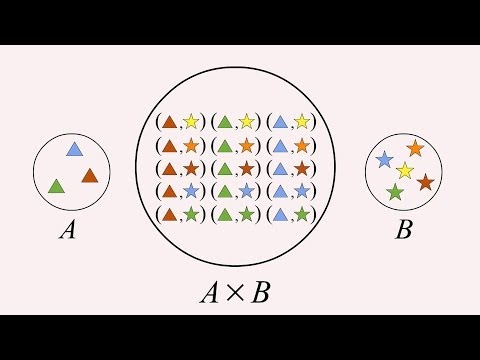
The Cartesian product of 2 graphs, G and H, is itself a graph with vertex set equal to the cartesian product of the vertex sets of graphs G and H, with order equal to the product of the orders of graphs G and H, and adjacencies between vertices defined as follows: two vertices (u,u' ) and (v,v' ) are adjacent in G * H if and only if either u = v and u' is adjacent to v' in H, or u' = v' and u is adjacent to v in G.

The Cartesian product of 2 graphs is just one of many graph products, which are operations on graphs that create new graphs from factor graphs.

By learning about graph products, we can change our perspective on what graphs are. Just like numbers multiply and divide, in addition to representing a constant quantity, graphs, too, can act upon each other through graph products. This video gives you a visual perspective on the cartesian product of 2 graphs and walks you through several examples so you know how to calculate this product yourself for any two graphs.

Thanks for watching!

*******************************************************************************************************
If you want to learn more about graph products, I highly recommend the following book:

Note: This is my Amazon Affiliate link. As an Amazon Associate I may earn commissions for purchases made through the link above.

00:00 Review
01:05 Definition
03:15 Example 1
06:53 Example 2
08:51 Intuition

[golden_smaug]

Books' definitions are usually quite cumbersome but thanks to this video I got a good grasp of what it is a cartesian product, thanks! :)

[davideographer]

Very intuitive explanation! Every other explanation I found was too formal and esoteric, devoid of any meaningful examples, but your video clarified it wonderfully! Thanks 👍

[mahaan]

This video taught me about the Cartesian product of graphs the best way 😍
Thank you sir!

[rembautimes]

Very well explained. Thanks a lot for taking the effort to make this topic clear

[garchompplush]

Loving this video so badly. Thank you man

[mahakaransandhu]

Great video, very clear explanation, thank you!

[atrsankaralingamvalarmathi]

Excellent explanation... Could you plz make some videos regarding algebraic graphs... thank you

[MathwithWaqasShah]

great explanation sir. really helpful.
you earned my subscription.
thanks

[VitalSine]

0:00 Review
1:05 Definition
3:15 Example 1
6:53 Example 2
8:51 Intuition

[PhilBoswell]

Nice video, but your outro is very loud compared to the rest, it comes as a nasty shock on headphones 🔊

I look forward to the next one.

[رِهامعدنانحنونأبوالهيل]

Hi teacher can you help me

prove that G×Hisomorphism H×G