Introduction to Laplace and Poisson Equations

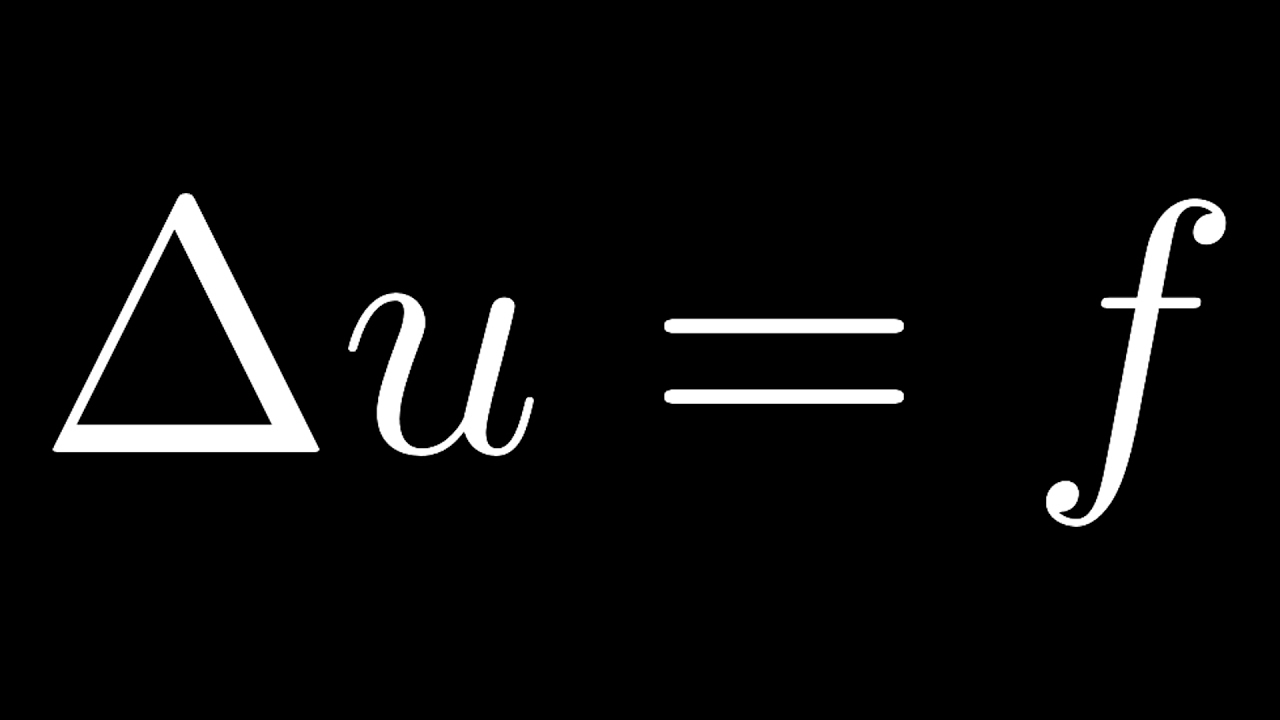
preview_player
Показать описание
  1. MathTheBeautiful
  2. Partial Differential Equations
  3. Laplacian
  4. Eigenvalues
  5. Diffential Operator
  6. Laplace Equation
Рекомендации по теме
Introduction to Laplace 0:16:45

Introduction to Laplace and Poisson Equations

Laplace's Equation and 0:17:55

Laplace's Equation and Poisson's Equation

introduction to Laplace, 0:33:05

introduction to Laplace, Poisson equations

Laplacian intuition 0:05:31

Laplacian intuition

Introduction to PDE's. 0:10:02

Introduction to PDE's. 18. Laplace and Poisson equations. Preliminaries.

ECE221: Laplace's Equation 0:12:42

ECE221: Laplace's Equation and Poisson's Equation

Poisson's and Laplace 0:12:19

Poisson's and Laplace Equations: Derivations and Explanations

Uniqueness Theorems in 0:04:46

Uniqueness Theorems in Electrostatics | Laplace and Poisson Equation

Poisson's Equation and 0:09:59

Poisson's Equation and Laplace's Equation

2_8 LaPlace and 0:16:49

2_8 LaPlace and Poisson Equations

EMT Chapter 6: 0:06:18

EMT Chapter 6: Laplace, Poisson, and Uniqueness Theorem (Part 1 Introduction to Laplace and Poisson)

2.3.3 Poisson's Equation 0:02:23

2.3.3 Poisson's Equation and Laplace's Equation

Laplace and Poisson's 0:11:43

Laplace and Poisson's equation Introduction

B.V. Problems - 0:08:19

B.V. Problems - Introduction: Poisson and Laplace Equations

Poisson and Laplace 0:18:03

Poisson and Laplace Equations

Poisson's Equation for 0:12:12

Poisson's Equation for Beginners: LET THERE BE GRAVITY and How It's Used in Physics | Part...

Poisson and Laplace 0:03:22

Poisson and Laplace equations

Poisson's and Laplace 0:17:39

Poisson's and Laplace _ 03 _ Electromagnetic Fields

Laplace's Equation and 0:15:32

Laplace's Equation and Potential Flow

This chapter closes 0:00:16

This chapter closes now, for the next one to begin. 🥂✨.#iitbombay #convocation

Laplace's and Poisson 0:08:55

Laplace's and Poisson Equations

Problem 2.29 - 0:00:37

Problem 2.29 - Electric Potential, Poisson's & Laplace's Equations: Introduction to El...

Introduction to Laplace 0:05:16

Introduction to Laplace transforms

lec25 Laplace and 0:32:57

lec25 Laplace and Poisson equations-8

Комментарии
Автор

People like you inspire me a lot. Never stop teaching professor!

jagdishannepu
Автор

“you will quite quickly, or relatively slowly, depending on your material properties average out” LOL I admire your approach professor, you are such an inspiration, thank you for sharing such passion with us

Omar.Alamoudi
Автор

Finally, A video where the real use of Laplace equations is found in a totally realistic way.

mohithmaruvada
Автор

This type of math prof is like Osmium, rare af and precious.

lLl-flrv
Автор

wow.. i love his clarity in visualizing things with MATHS

jhalakdhakal
Автор

Professor MathTheBeautiful, thank you for an awesome Introduction and Analysis to the classical Laplace and Poisson Equations in Partial Differential Equations. This is an error free video/lecture on YouTube.

georgesadler
Автор

What I have learned make so much more sense now! THANK YOU! I am watching this before my final, and I LOVE YOUR VIDEO!

gerryg
Автор

Just a thought!! Harmonic is when there is no accumulation of energy. A harmonic musical is usually melodious and nice to listen to because the energy is dissipated continuously without interfering with the incoming sound and this doesn't create interference or unpredictable peaks in the sound. Hence its more melodious!

curiousbit
Автор

What an explanation! Thank you so much...can you please prescribe some good textbooks for these topics

ManpreetKaur-ryvz
Автор

thanks I really enjoyed all the wonderful science analogies to the math equations!

sdsa
Автор

it really does initiate some intuiton about the subject. much appreciated. thank you!

determinnt
Автор

This is just great. What a great professor!!!

victora.
Автор

Great video! I can see you channeling Feynman

matthewkiely
Автор

Thank you very much! Great explanation

pedrogaleano
Автор

there's a difference between your core body temperature & that of your extremities like your arm

godsrighteousness
Автор

Thank you for the awesome video & nice camera as well

pinoji
Автор

6:30 a function is harmonic if the laplacian is zero.

davidkwon
Автор

Isn't a candle and the heat from a person kind of the same thing? Don't understand why one would be explained with lagrange while the other with poisson. They seem like the same thing to me, an influx in temperature

tandlose
Автор

Why is the video wide screen...so much black space

TowerfHeaven
Автор

Pause at 02:52 and you will see an angel :)

scitwi