Calculus 1, Lec 19B: Multivariable Function Graphs, Partial Derivatives, Implicit Differentiation

Sorry about all the mistakes in this lecture.

(0:00) -cos^(-1)(x) is a vertical translation of sin^(-1)(x), so they are both antiderivatives of 1/sqrt(1 - x^2).
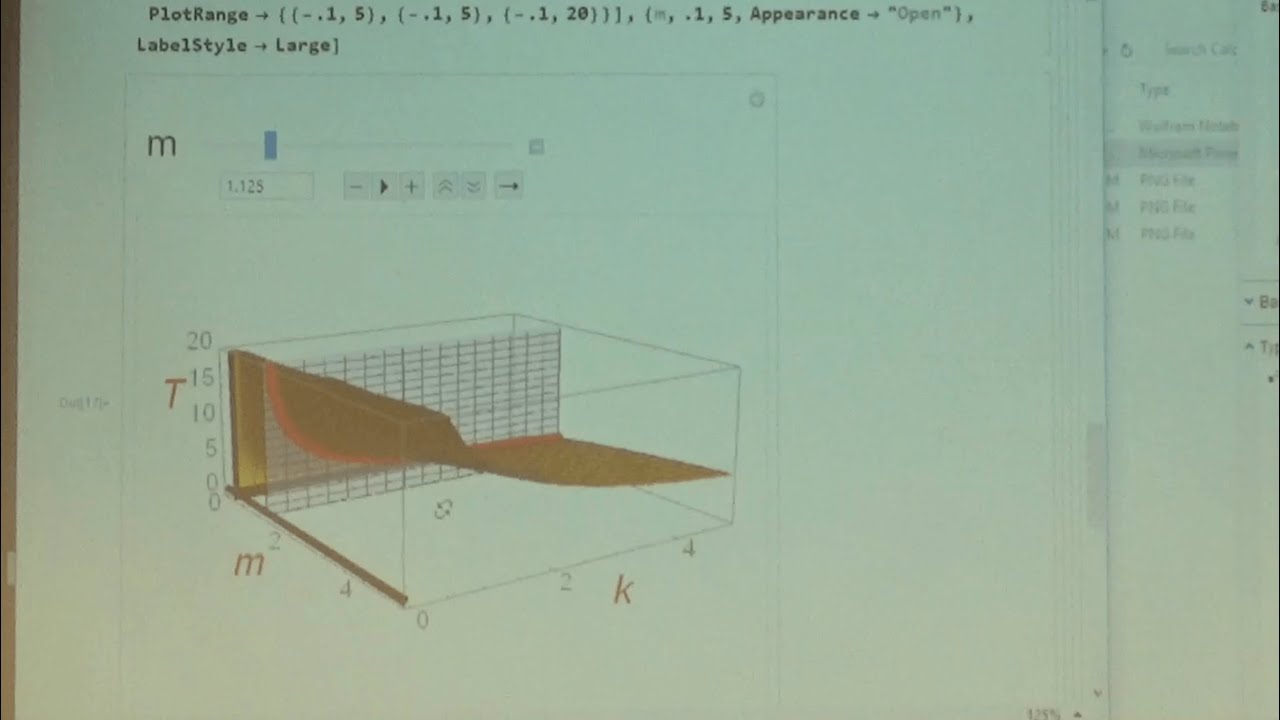
(1:29) Higher-dimensional graphs of period T and frequency f of a mass on a spring as functions of the mass m and the spring constant k. Graphs made in Mathematica.
(7:59) The compound interest formula can be thought of as giving the final amount A as a function of 4 variables: P (the principal), r (the nominal annual interest rate), n (the number of compounding periods per year), and t (the time, in years). Find the partial derivative with respect to each of the 4 variables, even though n is technically discrete instead of continuous.
(13:57) Use logarithmic differentiation to find the (messy) derivative with respect to n.
(19:47) Level curves of a function z = f(x,y) are often not graphs of functions. Locally they can still be graphs of implicit functions (rather than explicit functions where y is solved for). We still might like to find their slopes and tangent lines at various points. This is often best done with implicit differentiation.