filmov
tv
Trigonometry - Find The Range of sin^4x + cos^4x

Показать описание
Trigonometry - Find The Range of sin^4x + cos^4x
How to find domain and Range of Sine, Cosine and Tangent
How to find the range of the sine and cosine graph
Domain and Range of Trigonometric Functions - Part 1 | Don't Memorise
Graphs of Inverse Trigonometric Functions (1 of 2: Thinking through domain & range)
Trig Visualized: One Diagram to Rule them All (six trig functions in one diagram)
Find domain and range of sine inverse (5x+1)
Domain, Range, and Signs of Trigonometric Function
Inverse Trigonometric Functions
Example: Graph, domain, and range of sine function | Trigonometry | Khan Academy
Master How to determine the domain and range of the inverse trigonometric functions
Trigonometric Range | Decoded 🧐 | JEE Main 2022 | JEE Maths | Vedantu JEE
Evaluating Inverse Trigonometric Functions
TR-21: Domain and Range of Trig Functions (Trigonometry series by Dennis F. Davis)
Six Trigs in 60 Seconds! #math #trigonometry
And You Thought Trigonometry Was Pointless…
Find Possible Angles Between 0 to 360 degrees for Given Trigonometric Ratio
Inverse tan domain and range | Trigonometry | Khan Academy
Basic Properties of Trigonometric Functions (Precalculus - Trigonometry 8)
📚 How to find the domain and range of the trigonometric function, sine, cosine, and tangent
Find the Domain and Range of trigonometric functions | fully explained
Find the domain range and period for cosecant and secant functions
Find domain and range of cos tan inverse x AP Calculus Composite Trig Function
How To Graph Trigonometric Functions | Trigonometry
How To Use Reference Angles to Evaluate Trigonometric Functions
Комментарии
 0:12:48
0:12:48
 0:04:25
0:04:25
 0:05:49
0:05:49
 0:07:53
0:07:53
 0:04:15
0:04:15
 0:05:13
0:05:13
 0:08:30
0:08:30
 0:06:54
0:06:54
 0:09:22
0:09:22
 0:13:16
0:13:16
 1:12:26
1:12:26
 0:22:47
0:22:47
 0:05:23
0:05:23
 0:01:00
0:01:00
 0:01:00
0:01:00
 0:04:37
0:04:37
 0:09:44
0:09:44
 1:10:54
1:10:54
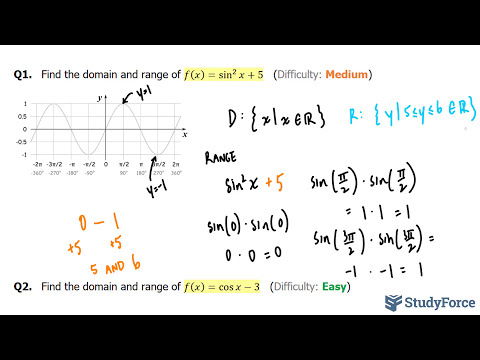 0:06:56
0:06:56
 0:36:38
0:36:38
 0:06:20
0:06:20
 0:07:55
0:07:55
 0:22:37
0:22:37
 0:10:59
0:10:59