filmov
tv
Let's Evaluate An Algebraic Expression
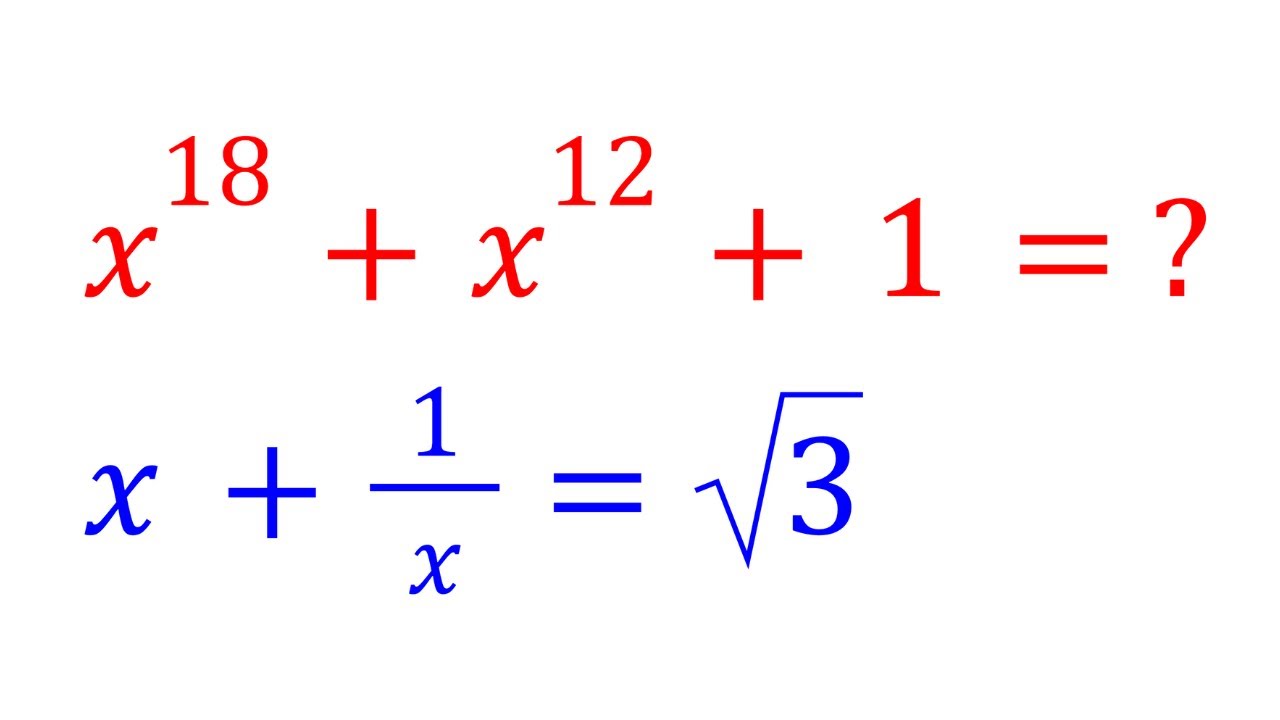
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#algebra #polynomials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#algebra #polynomials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
How To Evaluate Algebraic Expressions
Let’s Evaluate the ALGEBRAIC Expression – step by step
Let's Evaluate An Algebraic Expression
Algebraic Expressions Made Easy: Learn How to Evaluate Them
Let's Evaluate An Algebraic Expression
ALGEBRA | EVALUATE ALGEBRAIC EXPRESSIONS WITH GIVEN VALUES | Example 1
Evaluating Algebraic Expressions | Let's Substitute!
Evaluating Algebraic Expressions with Multiple Variables
MyDreamConnect Bootcamp (ADDITIONAL SUPPORT Events)
Evaluating Algebraic Expressions
Evaluating Algebraic Expressions: Part 2 Help Video 1 - Algebra for Teens!
Evaluating Algebraic Expression
HOW TO EVALUATE ALGEBRAIC EXPRESSION WITH FRACTIONS|CHANG DAYAN
🤔How to simplify algebraic expressions??? Algebraic Expressions/Short Tricks #shorts #shortsfeed
Write and Evaluate Algebraic Expressions
7 Math - Algebraic expressions - The value of an algebraic expression
Algebraic Evaluation #shorts #maths #algebra #evaluation #mathpractice
10-12 Math Unit 4 Lesson 3 Activity 4 - Evaluating Algebraic Expressions
Evaluating Expressions || Algebra-1 with Mr. Peters
Evaluating Algebraic Expressions in Fractional Form | Math with Mr. J
Evaluating algebraic expressions
How to Simplify an Expression: A Beginner's Guide | Algebraic Expressions | Math with Mr. J
simple math
Year 7 Evaluating Algebraic Expressions
Комментарии
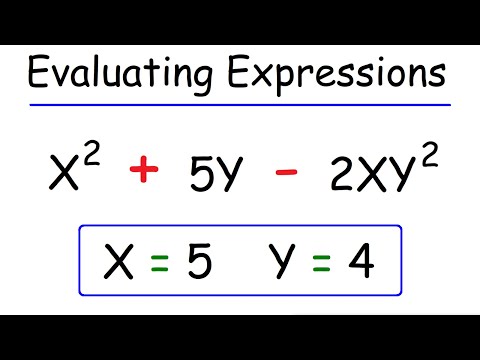 0:13:55
0:13:55
 0:09:10
0:09:10
 0:08:15
0:08:15
 0:00:53
0:00:53
 0:08:48
0:08:48
 0:04:22
0:04:22
 0:01:49
0:01:49
 0:01:00
0:01:00
 3:58:00
3:58:00
 0:06:06
0:06:06
 0:03:57
0:03:57
 0:05:51
0:05:51
 0:09:27
0:09:27
 0:00:16
0:00:16
 0:20:46
0:20:46
 0:06:11
0:06:11
 0:00:52
0:00:52
 0:04:54
0:04:54
 0:08:47
0:08:47
 0:04:58
0:04:58
 0:01:58
0:01:58
 0:55:18
0:55:18
 0:00:12
0:00:12
 0:05:31
0:05:31