filmov
tv
Manifolds Part 2.wmv

Показать описание
Here we describe what might be called the Macroscopic structure of Manifolds. Includes a detailed diagram of the features of M. Construction of Charts aka Coordinate Patches on M. The atlas of charts and the C-infinity manifold condition on the common boundaries of adjacent charts. Construction of a continuous bijective map between Charts of M and the Cartesian product space of real numbers, R^n. Sub-Manifolds. Construction of a Linear Space of points in R^n. Epsilon neighborhoods in R^n as linear spaces of differentials. Construction of differentials on M.
Manifolds Part 2.wmv
Calculus on Manifolds for Thermodynamics Part 2rev.wmv
Manifolds Part 1.wmv
Analysis II Lecture 15 Part 2 flows on manifolds
Manifolds Part 3 A.wmv
Manifolds Part 4.wmv
INTRO to Manifolds Video Collection.wmv
Calculus on Manifolds for Thermodynamics Part 1.wmv
Analysis II Lecture 13 Part 1 the differential for functions on manifolds
RS2 Manifold at WOT.wmv
Analysis II Lecture 13 Part 2 Jacobians for differentiable functions on manifold
Linear Spaces for Manifolds Part 1.wmv
Merge Collector Intake Manifold Build Part 2 CA18DET
TVR TITT 6 Tunnel near Mermaid Theatre Part 2.wmv
Manifolds 2.2 : Examples and the Smooth Manifold Chart Lemma
Topological two-manifolds
SS20 Assembly Instructions Part 2.wmv
'51 Chevy split manifold; part 1
Rooftop Equipment Vee Manifold for Applying Two Part Adhesives Big Rock Supply
Manifolds For Thermodynamics Pt1.wmv
Is it worth it? | 3.7L Intake Manifold and Throttle Body | 2008-2012 Honda Accord
Explanation of some of our new intake manifolds and parts
Harley Davidson Evolution Carburetor rebuild Part 2, including intake manifold
C. De Lellis - Center manifolds and regularity of area-minimizing currents (Part 1)
Комментарии
 0:17:38
0:17:38
 0:16:21
0:16:21
 0:22:45
0:22:45
 0:10:31
0:10:31
 0:13:16
0:13:16
 0:14:04
0:14:04
 0:01:54
0:01:54
 0:18:23
0:18:23
 0:09:03
0:09:03
 0:00:29
0:00:29
 0:10:40
0:10:40
 0:20:34
0:20:34
 0:34:48
0:34:48
 0:00:27
0:00:27
 0:14:05
0:14:05
 0:09:40
0:09:40
 0:08:32
0:08:32
 0:01:55
0:01:55
 0:01:41
0:01:41
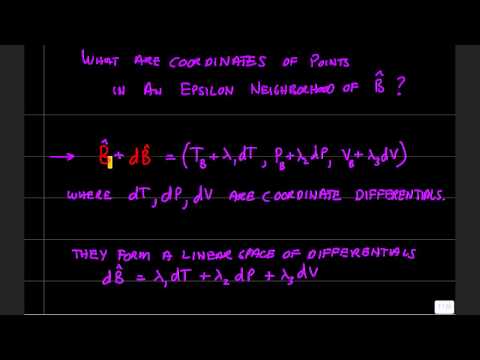 0:22:21
0:22:21
 0:04:51
0:04:51
 0:07:07
0:07:07
 0:51:21
0:51:21
 1:50:07
1:50:07