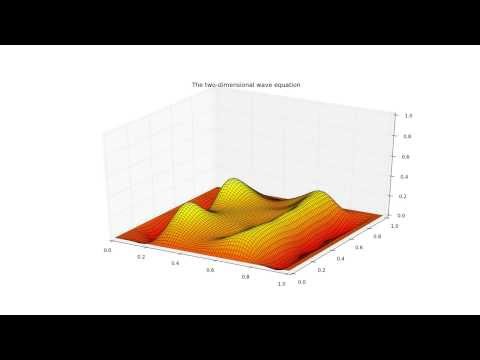
Solution of Two Dimensional Wave Equation using Method of Separation of Variables

In this educational video, we delve into the Solution of Two Dimensional Wave Equation using Method of Separation of Variables and Dirichlet conditions through easy an detailed procedure.

Reference Video :
40: Solution of ODE Involved in the Solution of PDE

📚 Key Topics Covered:
Understanding the 2-D Wave Equation
Method of Separation of Variables Demystified
Step-by-Step Solution Walkthrough
Insights into Dirichlet Conditions
Explaining the solution steps

🎓 Who Is This For?
Students studying advanced mathematics or physics
Enthusiasts exploring partial differential equations
Educators looking for teaching resources

🤔 Frequently Asked Questions (FAQs):
Q1: Find the general solution of wave equation when membrane is fixed for all times. The initial displacement of membrane is given by f(x,y) and initial velocity is is given by g(x,y).

Q2: solve two dimensional wave equation with homogeneous boundary conditions.

Q3: solve two dimensional wave equation with Dirichlet boundary conditions.

Q4: find the transverse vibrations of the thin rectangular elastic membrane . The initial displacement of membrane is given by f(x,y) and initial velocity is is given by g(x,y).

Q5: Find the solution of two dimensional wave equation with non-zero initial velocity.
Q6: Find the solution of two dimensional wave equation with non-zero initial displacement.

More related Videos:

37. Solution of Wave Equation With Fixed Endpoints and Zero Initial Velocity | Dirichlet Conditions

38. Solution of Wave Equation With Fixed Endpoints and Non- Zero Initial Velocity

39. Solution of Wave Equation with Free Ends | Separation of variables | Neumann Conditions

33. Method of Separation of Variables for First Order PDE | Complete Concept

34. Complete Review of Boundary and Initial Conditions in Partial Differential Equations

Partial Differential Equations (Full Course)

👍 If you find this tutorial helpful, don't forget to like, share, and subscribe for more educational content. Drop your questions in the comments section below, and let's unravel the mysteries of the 2-D Wave Equation together! 🔍🧠

#Mathematics #WaveEquation #DirichletConditions #Tutorial #Education #Physics #MathTutorial #Partialdifferentialequation
#EngineeringMathematics #BSCMaths

More in this video:
What is the method of separation of variables for two dimensional wave equation?
How does the separation of variables technique work for solving two dimensional wave equation?
What are the steps involved in using separation of variables to solve two dimensional wave equation?
Can you provide an example or application where the method of separation of variables is used to solve a two dimensional wave equation?
method of separation of variables
two dimensional wave equation
two dimensional wave equation solution technique
method of separation for two dimensional wave equation
solving second order PDE using separation of variables
steps for separation of variables for two dimensional wave equation
variable separation method for two dimensional wave equation
problems on method of separation of variables for two dimensional wave equation in hindi
method of separation of variables in hindi
wave equation
partial differential equations
solution of two dimensional wave equation
Dirichlet boundary conditions
two dimensional wave equation solution
solution to the two dimensional wave equation
two dimensional wave equation separation of variables
fourier series for two dimensional wave equation
separation of variables wave equation 2d
two dimensional wave equation
solution of two dimensional wave equation
solution of wave equation in two dimensions
wave equation solution
2d wave equation solution
two dimensional wave equation separation of variables
solution of wave equation using separation of variables

My Social Media Ends:
Instagram:
Facebook:

[khalaimakhlook]

first initial condition ko solve karnay kay baad hum summation ko kiu kha gay?