Factoring using distributive property

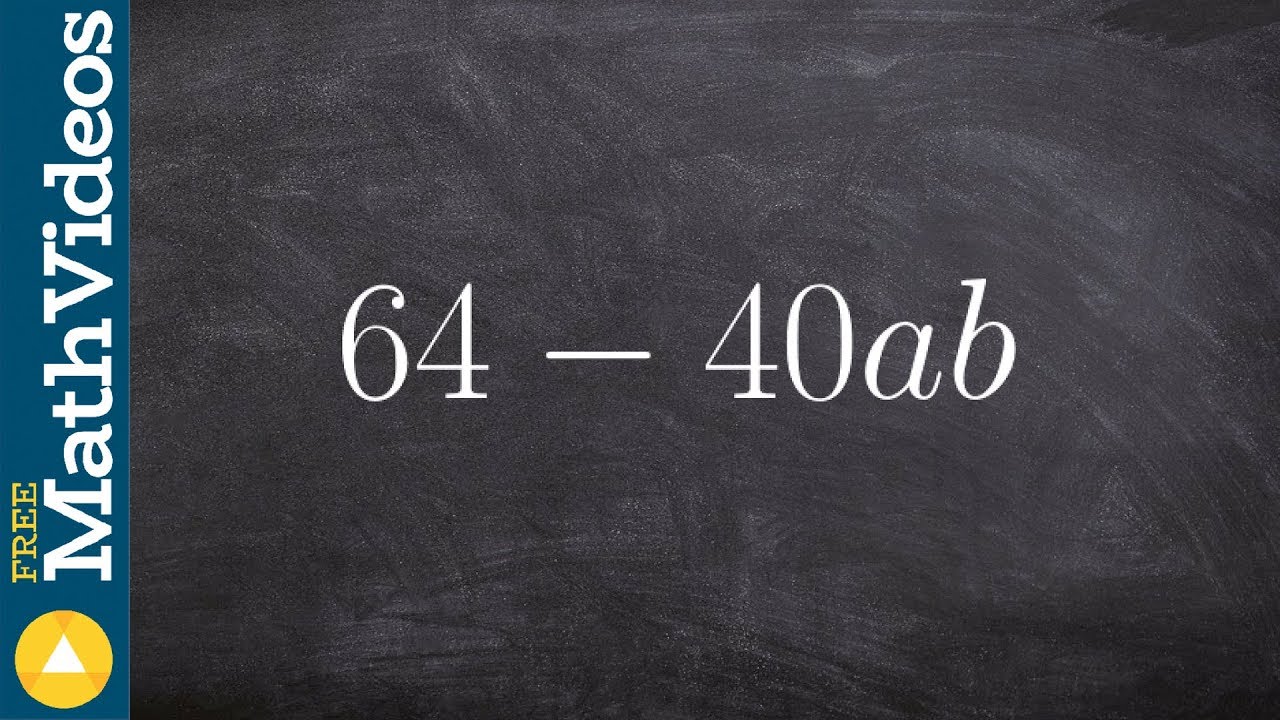
Показать описание

Keywords

👉 Learn how to factor polynomials by GCF. A polynomial is an expression of the form ax^n + bx^(n-1) + . . . + k, where a, b, and k are constants and the exponents are positive integers. To factor an algebraic expression means to break it up into expressions that can be multiplied together to get the original expression.
To factor a polynomial by GCF, all we need to do is to identify the GCD (the greatest expression that can divide all the terms of the quadratic without remainder). After identifying the GCD we then express the original quadratic as a product of the GCD and the factors which when multiplied to the GCD yields the original quadratic.

Organized Videos:
✅How to Factor a Polynomial
✅How to factor a polynomial | Learn about
✅How to factor out the GCF from a polynomial
✅How to factor a perfect square polynomial
✅How to factor a polynomial by difference of two squares
✅How to factor a polynomial by sum or difference of two cubes
✅How to factor out an expression from a polynomial
✅How to factor a polynomial by grouping with two variables
✅How to factor a polynomial by grouping
✅How to factor a polynomial to a higher power

Connect with me:

#polynomials #brianmclogan