filmov
tv
If x=ⅇ^cos 2t and y=ⅇ^sin 2t , prove that ⅆy/ⅆx=−ylogx/xlog y | jee mains important derivatives
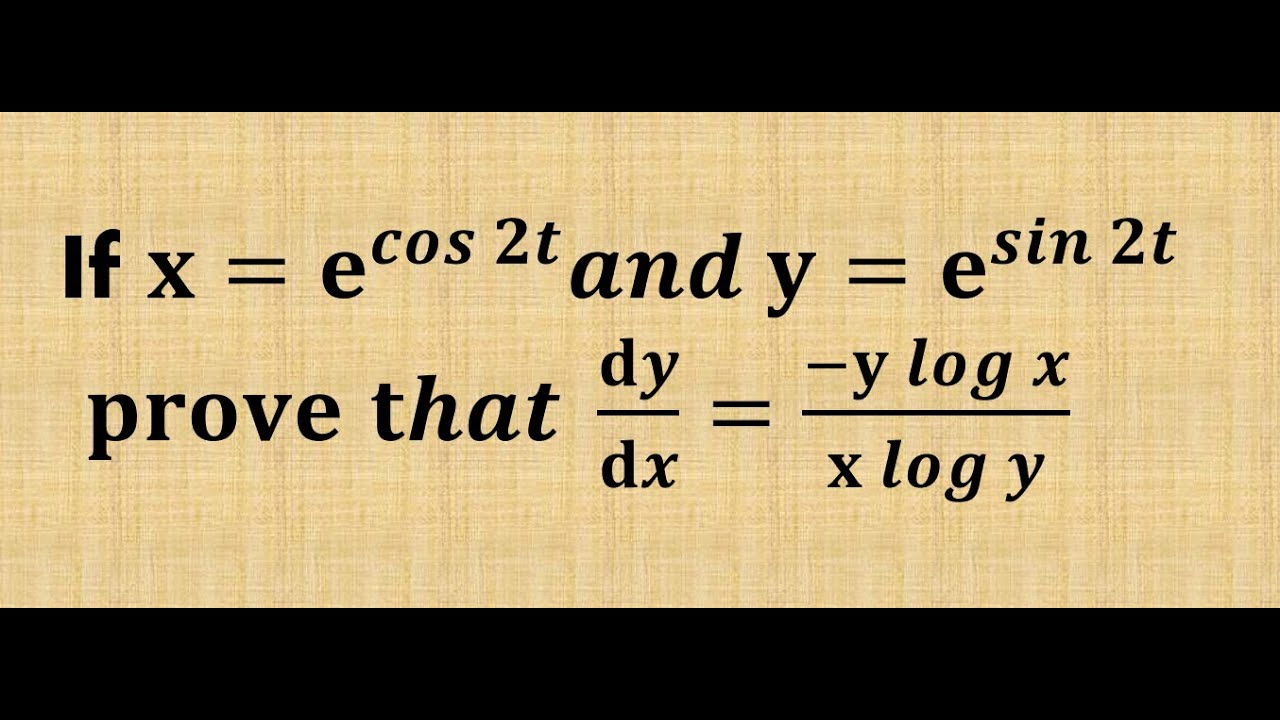
Показать описание
in this video, we will learn how to solve
1)If x=ⅇ^cos 2t and y=ⅇ^sin 2t , prove that ⅆy/ⅆx=−ylogx/xlog y
2)jee mains differentiation problems
3) important problems on derivatives
4) class 11 derivatives important problems
5) class 12 derivatives important questions
6)how to solve derivatives easily
7) famous derivative problems
8) previous years jee problems
9) important board problems in maths
10) important differentiation problems for boards
11) problems on chain rule in derivatives
12) problems on product rule
#jeeadvance #maths #jeemains #class11 #class12 #importantquestions #previousyearquestions #differentiation #derivatives #apmaths #tsmaths # apmaths #tsmaths #emcet #cuet
1)If x=ⅇ^cos 2t and y=ⅇ^sin 2t , prove that ⅆy/ⅆx=−ylogx/xlog y
2)jee mains differentiation problems
3) important problems on derivatives
4) class 11 derivatives important problems
5) class 12 derivatives important questions
6)how to solve derivatives easily
7) famous derivative problems
8) previous years jee problems
9) important board problems in maths
10) important differentiation problems for boards
11) problems on chain rule in derivatives
12) problems on product rule
#jeeadvance #maths #jeemains #class11 #class12 #importantquestions #previousyearquestions #differentiation #derivatives #apmaths #tsmaths # apmaths #tsmaths #emcet #cuet
0:10:00
If x=ⅇ^cos 2t and y=ⅇ^sin 2t , prove that ⅆy/ⅆx=−ylogx/xlog y | jee mains important derivatives...
0:14:23
JEE 2nd way if x=e^cos(2t) & y=e^sin(2t) prove that dy/dx=ylog(x)/(x log(y))
0:02:42
If \\(x=e^{\\cos 2 t}\\) and \\(y=e^{\\sin 2 t}\\), prove that \\(\\frac{d y}{d x}=-\\frac{y \\l....
0:04:14
If x=e^cos 2 t and y=e^sin 2 t, prove that d y/d x=-y log x/x log y. Given!- x=e^cos 2 t and y=e^...
0:01:31
If `x=cos(2t)and y=sin^(2)t`, then what is `(d^(2)y)/(dx^(2))` equal to?
0:05:30
If `x=2 cos t+cos 2t` and `y=2 sin t-sin2t`, then the value of `(dy)/(dx)` at `t=(pi)/(4)` is -
0:01:16
partial derivatives e^xcos(y) | e^x*cos(y) | partial derivatives | silent math
0:05:46
Differentiation of x=e^(2t)cos(t) and y=e^(2t)sin(t).
0:01:54
`x=e^t (sin t + cos t ),y=e^t(sin t -cos t)`
0:04:36
Arc Length of Parametric Curve: x = e^(2t)cos(2t) ; y = e^(2t)sin(2t) ; t varies from 0 to Pi
0:01:56
Q3 | Find dy/dx , x = sin t , y = cos 2t
0:02:07
If ` xsin t,y =cos 2t ,then (dy)/(dx) =`
0:00:10
12th Derivative x = 2cos t + cos 2t , y = 2sin t - sin 2t
0:06:42
Find the length of the curve x = e^(-t) cos t, y = e^(-t) sin t over [0, pi]. Parametric equations
0:03:16
How to differentiate the exponential function easily
0:13:40
If x=a sin 2 t(1+cos 2 t) and y=b cos 2 t(1-cos 2 t), show that (d y/d x)_a t t=π/4=b/aW
0:03:20
if cosy=x cos(a+y), then prove that dy/dx = cos²(a+y) /sina .
0:02:57
If ` x=e^(sin 3t), y=e^(cos,3t),then (dy)/(dx)=`
0:04:12
if x=cost(3-2 cos^2t) and y=sint(3-2 sin^2t ) find the value of dy/dx at t=π/4
0:14:32
Partial Differentiation || 𝒆^𝒙 (𝒙 𝑪𝒐𝒔 𝒚−𝒚 𝑺𝒊𝒏 𝒚) || VTU Maths || 22mat11 || Dr Prashant Patil...
0:02:34
How to differentiate e^(4x) (chain rule)
0:11:42
derivative x=cos³t/root cos2t, y=sin³t/root cos 2t, find dy/dx
0:00:35
differentiate y = e^cos x
0:01:29
Differentiate y=e^x cos^2 x
Комментарии