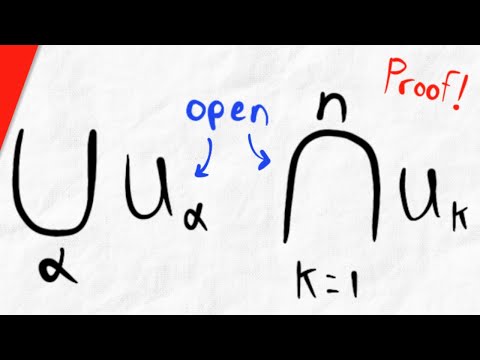
Infinite Intersection of Open Sets that is Closed Proof

Infinite Intersection of Open Sets that is Closed Proof

If you enjoyed this video please consider liking, sharing, and subscribing.

You can also help support my channel by becoming a member

Thank you:)

[charlesrodriguez]

This was a great video. You are clear, precise and rigorous. Thank you for the content!

[Ava-gslw]

this was a helpful video! i cried tears of joy when mine proved. thanks a million

[alexanderwhyte]

Nice video! Does this extend generally to any infinite intersection of open non-empty proper subsets? (in a complete metric space). I ask because I came across a lemma by Cantor which says that the infinite intersection of non-empty, compact, closed subsets is equal to a point x (which would be a closed set as in your example). I'm just wondering why it specifically mentions closed subsets. Your example here suggests to me that it should also be true for open subsets.

Edit: i found my mistake. With open sets, the point the sets are converging to could be outside of all of the sets e.g. from wikipedia: Ck = ( 0, 1 / k ) .

[darrenpeck]

Would infinite intersections be ok with the discrete topology, using the powerset as singletons would be open? Thank you for the great tutorial

[anaandreabn]

I really liked your video, I woul like a general proof, anyway U helped me a lot :)

[seal]

how is x more than 0 and less than 0 at the same time? isn't that supposed to be a contradiction? shouldn't there the infinite intersection be empty?

[muse]

why is (-1/n, 1/n) open in the real numbers?

[Arun-ozrq]

e that the intersectiou of any finite collection of open sets is open. Justify,
why the same not holds for infinite collection.