filmov
tv
Solve this System of rational Equations | Quick & Easy Explanation
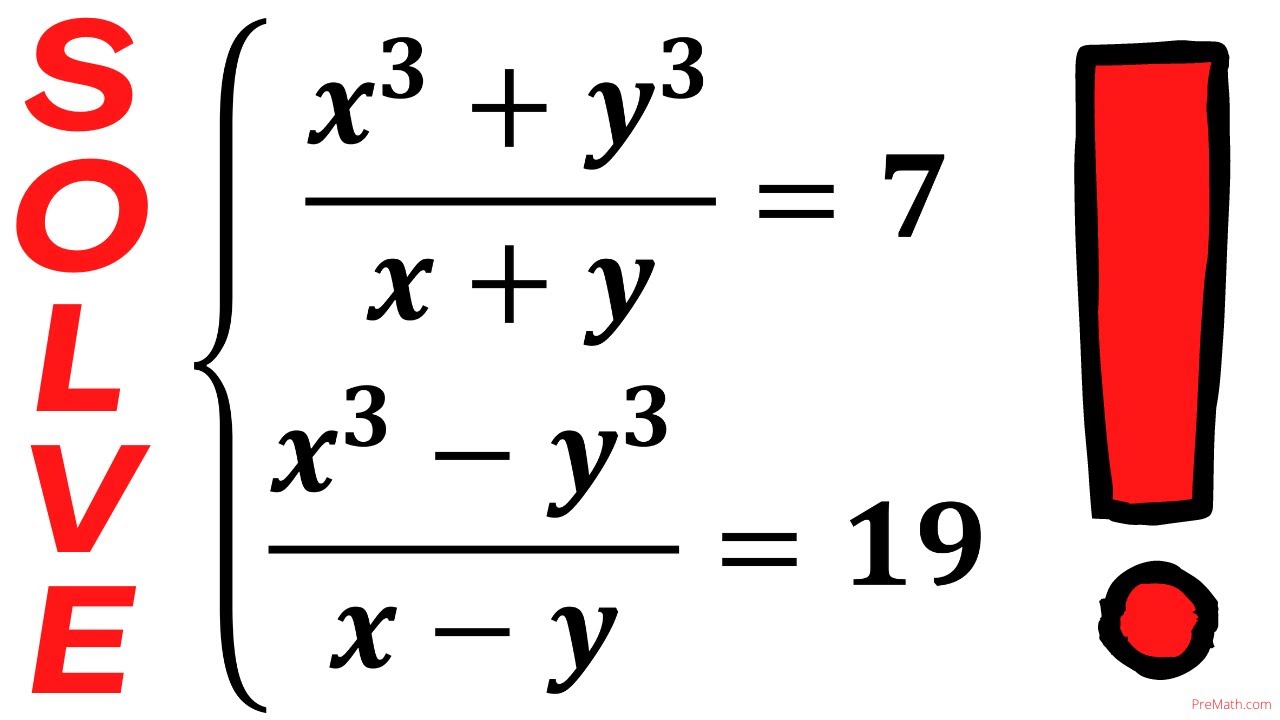
Показать описание
How To Solve Systems of Rational Equations - Algebra
Solving Rational Equations
Solve this System of rational Equations | Quick & Easy Explanation
Rational Inequalities
system of rational equations
Solving Systems of Rational Equations FG
Rational and Irrational Numbers
How To Solve Rational Equations
class 8th Chap-8 8.4 question 10
Why solving a rational inequality is tricky!
Solving a Rational System in Two Ways
A Functional System with Rational Functions
Ex: Solve a Rational Equation
Solving Systems of Rational Equations DE
Solving Rational Equations (Domain Restrictions)
Write Repeating Decimals 2.1666 as Rational Numbers
Can You Solve this Rational Equation? | Quick & Easy Explanation
What is a Rational Number? | Math with Mr. J
Solving Rational Equations With Fractions and Variables & Different Denominators - College Algeb...
Rational Numbers Explained | Math with Mr. J
How to Simplify Rational Expressions in Algebra
Solving Linear Rational Equations
An Intro to Rational and Irrational Numbers | Math with Mr. J
Solving Rational Equations
Комментарии
 0:10:21
0:10:21
 0:11:03
0:11:03
 0:08:09
0:08:09
 0:10:18
0:10:18
 0:09:43
0:09:43
 0:04:03
0:04:03
 0:05:54
0:05:54
 0:10:06
0:10:06
 0:04:20
0:04:20
 0:08:34
0:08:34
 0:12:02
0:12:02
 0:08:09
0:08:09
 0:04:29
0:04:29
 0:05:28
0:05:28
 0:02:45
0:02:45
 0:04:08
0:04:08
 0:09:53
0:09:53
 0:01:00
0:01:00
 0:17:32
0:17:32
 0:09:54
0:09:54
 0:01:00
0:01:00
 0:04:37
0:04:37
 0:17:31
0:17:31
 0:21:13
0:21:13