Elliptic Curve Cryptography Overview

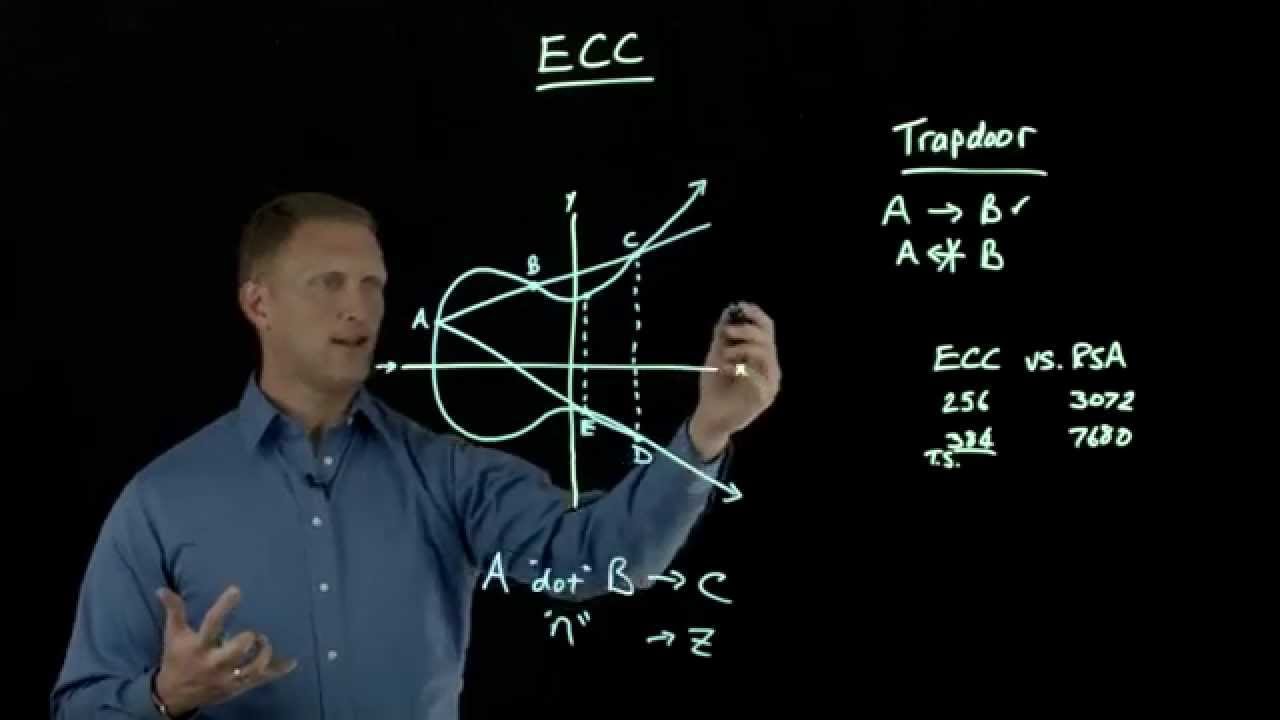
John Wagnon discusses the basics and benefits of Elliptic Curve Cryptography (ECC) in this episode of Lightboard Lessons.

Corrections:
02:24 As we all know, a prime number only has itself and 1 as factors. So, if you multiply two numbers together, the resultant number will at least have the two numbers you multiplied as factors…thus not making it prime. Technically speaking, the product of the two prime numbers in RSA is called a “semiprime” number because its only factors are 1, itself, and two prime numbers.

[bladi]

this is by far the best video i have come across. Simple, explained in layman's terms to beginners and under 15 minutes. rate this 10 out of 10

[PHTM]

It baffles me how people have the knowledge enough to 1) Come up with such ideas and most importantly 2) To code such applications that can do such complex things. The cryptographic world is so unique in so many ways, as us people many times take it for granted to ease of use in such applications since we can freely use them, but lord knows the backend behind all that computation

[MamoonSyed]

how is this guy so good at writing backwards...

[jony]

I never knew Matthew McConaughey was so good at math

[rettich]

2:20 wrong; the product of two prime numbers is always non-prime - because it has the two prime numbers as factors.

[bryanmccaffrey]

Love how you have to plug the BIG-IP thing at the end (someone has to pay for the Light Board. Well done, sir. You are a great presenter. One of the best I've come across.

[download]

It took me a while to realize and appreciate that this dude is writing backwards so we can read it forwards. Also, love your eyeballs. They are grade A, top-shelf eyeballs.

[BirSozben]

found this while prepping for the interview. thank you for such simple and yet practical explanation!

[gauthamj.m]

The best explanation that I got on Elliptic Curve Cryptography, great work John

[kaushikdr]

Protip: doing G + G is the equivalent of finding the point tangent to the curve at G! And since we already have added "two" points (the curve doesn't care if the points are different), the curve will only intersect at one other point!

[leonjones]

I have read about this before, but this is clearly explained! Well done.

[johngarnham]

This is a great easy-to-understand intro to ECC!

[rajd]

@2:26 -- when you take two prime numbers and multiply them, you WILL not get a BIG prime number. Sorry about that.

[nancode]

This video is, by far, the best video on eliptic curve criptography availiable... wish you could do more videos about this subject, congratulations for the amazing work!!!

[roshanbaliga]

Good introduction to ECC. In you intro to RSA you mention taking random prime numbers and multiplying them to get a really big prime number. The result is a really big composite number(not prime) that is hard to factorize.

[xoreign]

Fun fact, but my integral Calculus teacher in university was one of the creators of this :) Neil Koblitz. Very smart dude.

[antelope]

This was a fantastic intro to ECC, thanks for the clear explanation!

[Openwrt]

Excellent presentation. The Elliptic Curve in the video is drawn based on y^2=x^3-3x+5. The actual elliptic curve used in the algorithm will have much bigger prime numbers and will look much different. The same logic applies to either case, so it doesn't quite matter. Just for your information.

[grishnank]

I could not get this concept at all until I watched you're video. Thank you very much.

[curtstockman]

That was one very clear explanation of ECC. How can there be any thumbs down AT ALL?