Semi-norm (mathematics) | Wikipedia audio article

This is an audio version of the Wikipedia Article:


00:00:52 1 Definition
00:01:44 2 Notation
00:02:37 3 Examples
00:03:29 3.1 Absolute-value norm
00:04:21 3.2 Euclidean norm
00:05:14 3.2.1 Euclidean norm of a complex number
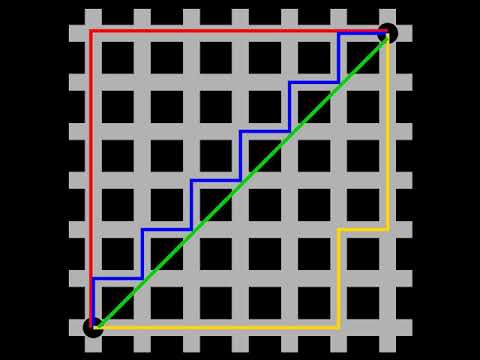
00:06:58 3.3 Taxicab norm or Manhattan norm
00:07:51 3.4 ip/i-norm
00:08:43 3.5 Maximum norm (special case of: infinity norm, uniform norm, or supremum norm)
00:09:36 3.6 Zero norm
00:11:46 3.6.1 Hamming distance of a vector from zero
00:12:39 3.7 Other norms
00:13:31 3.8 Infinite-dimensional case
00:14:24 4 Properties
00:15:16 5 Classification of seminorms: absolutely convex absorbing sets
00:16:34 6 Generalizations
00:20:04 7 See also
00:20:56 8 Notes
00:21:49 9 References
00:22:41 Generalizations
00:23:33 See also



Listening is a more natural way of learning, when compared to reading. Written language only began at around 3200 BC, but spoken language has existed long ago.

Learning by listening is a great way to:
- increases imagination and understanding
- improves your listening skills
- improves your own spoken accent
- learn while on the move
- reduce eye strain

Now learn the vast amount of general knowledge available on Wikipedia through audio (audio article). You could even learn subconsciously by playing the audio while you are sleeping! If you are planning to listen a lot, you could try using a bone conduction headphone, or a standard speaker instead of an earphone.

Listen on Google Assistant through Extra Audio:
Other Wikipedia audio articles at:
Upload your own Wikipedia articles through:
Speaking Rate: 0.7933315171807307
Voice name: en-US-Wavenet-B


"I cannot teach anybody anything, I can only make them think."
- Socrates


SUMMARY
=======
In linear algebra, functional analysis, and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to each vector in a vector space—except for the zero vector, which is assigned a length of zero. A seminorm, on the other hand, is allowed to assign zero length to some non-zero vectors (in addition to the zero vector). A norm must also satisfy certain properties pertaining to scalability and additivity which are given in the formal definition below.
A simple example is two dimensional Euclidean space R2 equipped with the "Euclidean norm" (see below). Elements in this vector space (e.g., (3, 7)) are usually drawn as arrows in a 2-dimensional cartesian coordinate system starting at the origin (0, 0). The Euclidean norm assigns to each vector the length of its arrow. Because of this, the Euclidean norm is often known as the magnitude.
A vector space on which a norm is defined is called a normed vector space. Similarly, a vector space with a seminorm is called a seminormed vector space. It is often possible to supply a norm for a given vector space in more than one way.