filmov
tv
The Rubik's Cube is a Calculator
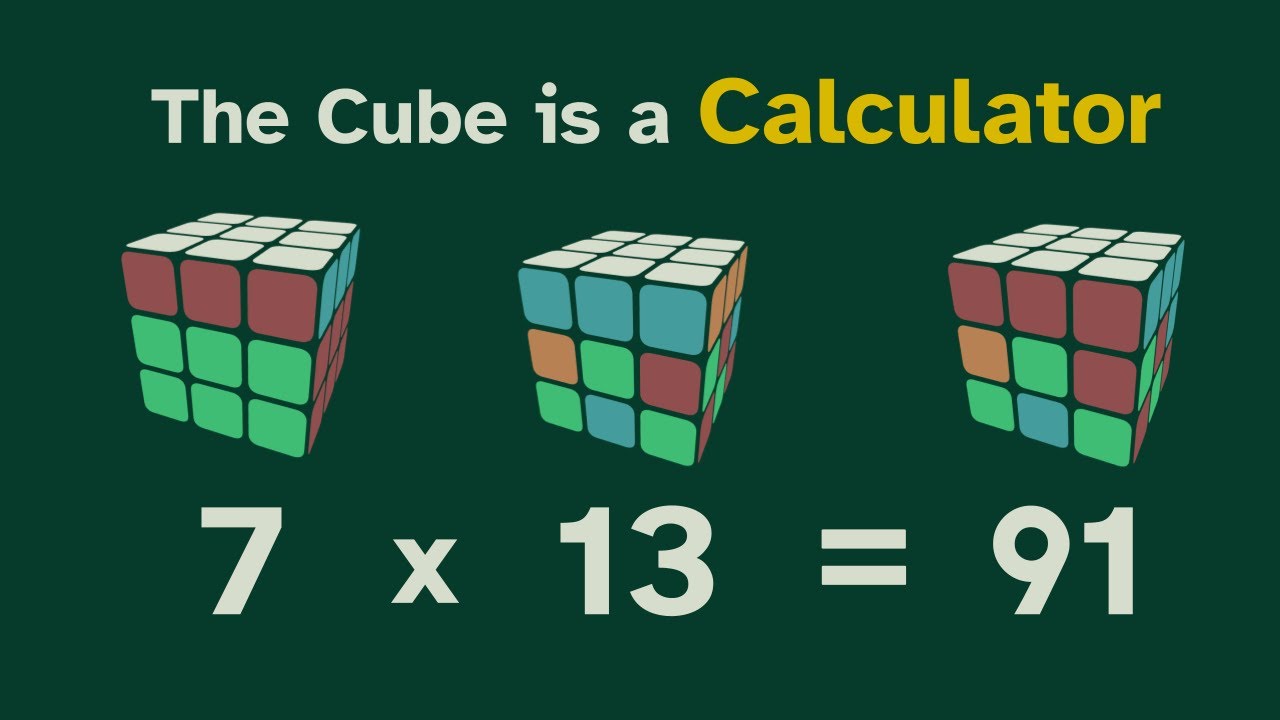
Показать описание
This video is an exploration of ways to apply modular multiplication to twisty puzzles.
Reference: Contemporary Abstract Algebra - Gallian
Reference: Contemporary Abstract Algebra - Gallian
Can You spot the Fake Rubik’s Cube? 🤔
Rubik’s Cube Collector Check #3
The Rubik’s cube challenge: Biggest, Smallest… Scariest! 👀😳🕸️ #wednesday #rubikscube
How to disassemble your Rubik's Cube
Normal Rubik’s Cube vs. GAN Cube 🧩
how to solve a rubik's cube fast #rubikscube
Best Rubik’s Cube Products!
Building a $70 Speedcube! 🛠️ #speedcubeshop #speedcube #rubikscube #cubing
Learn how to solve a rubik's cube 3x3 in 1 minute
EVERY RUBIK'S CUBE FROM 1x1 TO 19x19
GAN 15 MAGLEV 10 Years Edition magic trick 😱 #rubikscube #cubing #magic
EVERY Rubik’s Cube From 1x1 to 17x17 😎🥳 #shorts
World's Biggest Rubiks Cube Store!
Yiheng wants to know ZBLL! #rubikscube #viral #shorts #yihengwang
Rubik's Cube Tier List
Is This The World's Most Difficult Rubik's Cube?
Top 5 Illegal Rubik's Cubes 🚫
how to solve a rubik's cube 3x3 easy
what a phantom rubiks cube looks like
This Rubik’s cube CHANGES colors 😱
LIGHTEST vs. HEAVIEST Rubik's Cubes!
Can a CHEAP $2 Rubik’s Cube Be GOOD?
Rubik's Cage Explained
NEW WORLD RECORD RUBIKS CUBE 3×3 0.82 SEC#shorts #rubikscube #rubikscubechallenge #kingofcubers
Комментарии
 0:00:20
0:00:20
 0:00:30
0:00:30
 0:00:10
0:00:10
 0:00:30
0:00:30
 0:00:10
0:00:10
 0:00:18
0:00:18
 0:00:11
0:00:11
 0:00:41
0:00:41
 0:00:08
0:00:08
 0:00:39
0:00:39
 0:00:11
0:00:11
 0:00:33
0:00:33
 0:00:51
0:00:51
 0:00:21
0:00:21
 0:00:44
0:00:44
 0:00:18
0:00:18
 0:00:57
0:00:57
 0:00:33
0:00:33
 0:00:31
0:00:31
 0:00:39
0:00:39
 0:01:00
0:01:00
 0:00:55
0:00:55
 0:00:20
0:00:20
 0:00:20
0:00:20