filmov
tv
New Bounds for Large Values of Dirichlet Polynomials, Part 1' - James Maynard
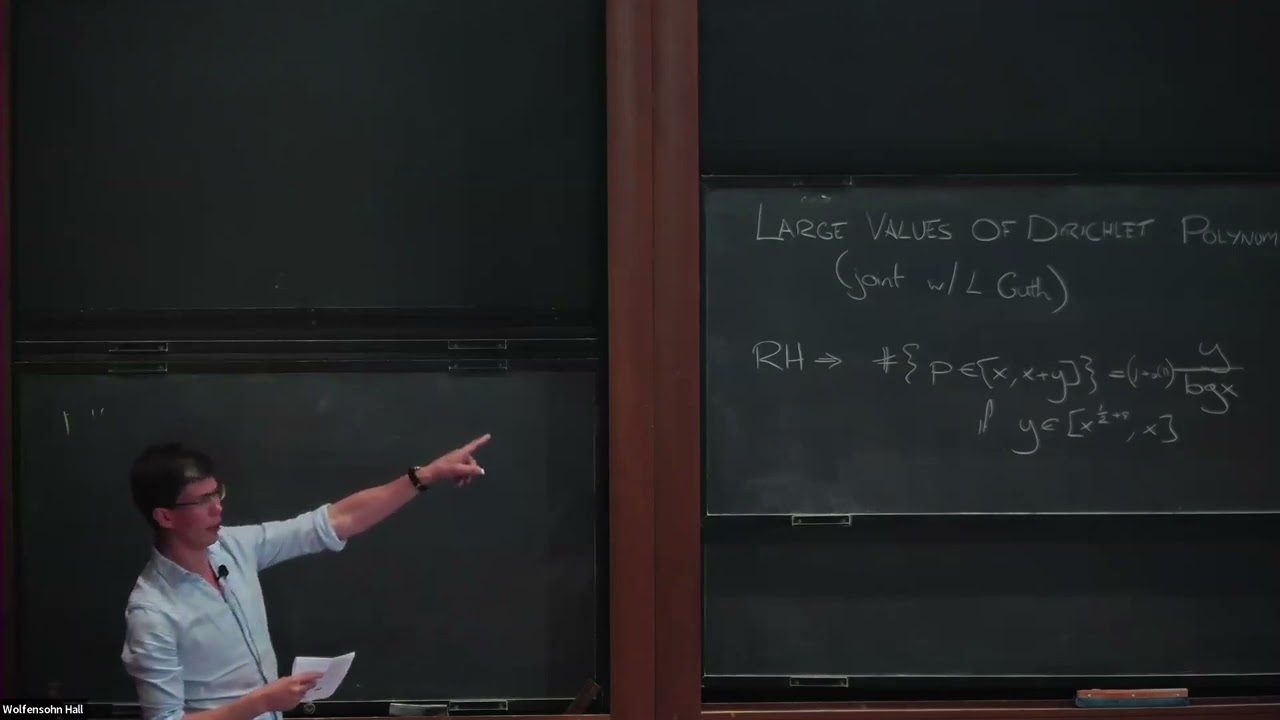
Показать описание
Visions in Arithmetic and Beyond: Celebrating Peter Sarnak's Work and Impact
Topic: New Bounds for Large Values of Dirichlet Polynomials, Part 1'
Speaker: James Maynard
Affiliation: University of Oxford
Date: June 04, 2024
Bounds for Dirichlet polynomials play an important role in several questions connected to the distribution of primes. For example, they can be used to bound the number of zeroes of the Riemann zeta function in vertical strips, which is relevant to the distribution of primes in short intervals. A Dirichlet polynomial is a trigonometric polynomial of the form
D(t) = \sum_{n = N}^{2N} b_n n^{it}.
The main question is about the size of the superlevel sets of D(t). We normalize so that the coefficients have norm at most 1, and then we study the superlevel set |D(t)| greater than N^\sigma for some exponent sigma between 1/2 and 1.
For large values of sigma, Montgomery proved very strong bounds for the superlevel sets. But for sigma \le 3/4, the best known bounds follow from a very simple orthogonality argument (and they don't appear to be sharp). We improve the known bounds for sigma close to 3/4. Work in progress. Joint with Larry Guth.
Topic: New Bounds for Large Values of Dirichlet Polynomials, Part 1'
Speaker: James Maynard
Affiliation: University of Oxford
Date: June 04, 2024
Bounds for Dirichlet polynomials play an important role in several questions connected to the distribution of primes. For example, they can be used to bound the number of zeroes of the Riemann zeta function in vertical strips, which is relevant to the distribution of primes in short intervals. A Dirichlet polynomial is a trigonometric polynomial of the form
D(t) = \sum_{n = N}^{2N} b_n n^{it}.
The main question is about the size of the superlevel sets of D(t). We normalize so that the coefficients have norm at most 1, and then we study the superlevel set |D(t)| greater than N^\sigma for some exponent sigma between 1/2 and 1.
For large values of sigma, Montgomery proved very strong bounds for the superlevel sets. But for sigma \le 3/4, the best known bounds follow from a very simple orthogonality argument (and they don't appear to be sharp). We improve the known bounds for sigma close to 3/4. Work in progress. Joint with Larry Guth.
New Bounds for Large Values of Dirichlet Polynomials, Part 1' - James Maynard
New Bounds for Large Values of Dirichlet Polynomials, Part 2 - Larry Guth
Why Shift the Bounds? U-Substitution with cos³(x) Explained
Bounds for the reduction number of primary ideals in dimension three
Broken Bound CEO James: Insights on MEMECoins and Long-Term Value in South Korea
STOC24 11 A 2 Constrained Submodular Maximization via New Bounds for DR Submodular Functions
Bounds Made Easy | Maths GCSE
Bounds for GCSE Maths
Bounds Challenge Question | GCSE Maths 2025
Upper And Lower Bounds
Upper & Lower Bounds | Number | Maths | FuseSchool
Upper bound (Maximum Value) of a Put Option - FRM
4.6.5 Chebyshev Bounds: Video
Raphael Steiner - New bounds for relatives of Hadwiger's conjecture
Finding the Upper and Lower Bounds | Maths GSCE
A time-space lower bound for a large class of learning problems - Ran Raz
Numbers - Upper and lower bounds (Video 3)
Bounds | GCSE Maths 2025
How to use upper and lower bounds
New Bounds on the Covering Density
GCSE Edexcel June 2022 Higher Paper 3 Q16 - Bounds | ExamSolutions
Key Skill - Calculate a further bound and specify the value to a suitable degree of accuracy.
Key Skill - Calculate a further bound for a given formula involving a subtraction.
Error bounds: solving problems involving maximum and minimum values
Комментарии
 1:12:19
1:12:19
 1:06:03
1:06:03
 0:03:44
0:03:44
 0:21:47
0:21:47
 0:03:55
0:03:55
 0:17:06
0:17:06
 0:00:59
0:00:59
 0:00:59
0:00:59
 0:00:59
0:00:59
 0:03:14
0:03:14
 0:04:32
0:04:32
 0:06:06
0:06:06
 0:10:22
0:10:22
 1:26:55
1:26:55
 0:01:00
0:01:00
 1:16:52
1:16:52
 0:03:12
0:03:12
 0:00:56
0:00:56
 0:11:15
0:11:15
 0:51:35
0:51:35
 0:02:13
0:02:13
 0:04:58
0:04:58
 0:03:02
0:03:02
 0:02:39
0:02:39