Maximum volume of a cone shaped cup (KristaKingMath)

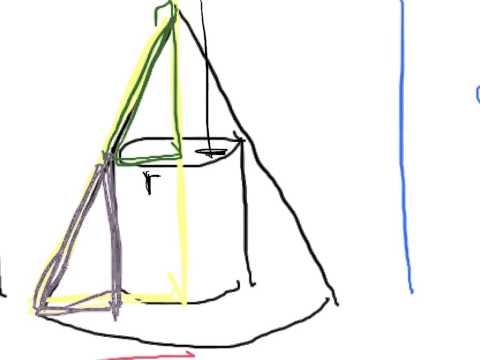
Learn how find the largest possible volume of a cone-shaped up made from a circular piece of paper with radius R, where a sector has been removed and sides CA and CB are joined together. To complete this optimization problem, you'll need to draw a picture of the problem and write down what you know. Then you'll imagine that you'll take a vertical slice of the cone shaped cup so that you can use the pythagorean theorem to relate the radius of the paper to the radius and height of the cone. Solve the pythagorean theorem, the constraint equation, for one of the variables so that you can plug it into the optimization equation, which will be the equation for the volume of the cone. Then simplify the equation for the volume, take the derivative and set it equal to 0 to solve for the height. Plug the height back into the pythagorean theorem to find the radius, then plug both values back into the volume equation to find the volume.

● ● ● GET EXTRA HELP ● ● ●

● ● ● CONNECT WITH KRISTA ● ● ●

Hi, I’m Krista! I make math courses to keep you from banging your head against the wall. ;)

Math class was always so frustrating for me. I’d go to a class, spend hours on homework, and three days later have an “Ah-ha!” moment about how the problems worked that could have slashed my homework time in half. I’d think, “WHY didn’t my teacher just tell me this in the first place?!”

[rootshell]

first off you have a very pleasant voice, secondly I tried many articles and the videos my teacher posted and asked him and your video/you were the only one that got me the correct answer and a simple way to get it everytime, thanks so much! I watched this vid once and got it right everytime. Clear, easy to follow, you take time and don't speed through the steps.

[scholar]

You have a very soft voice which is comfortable for the ear. You seem to explain in a nice and understand way thanks vincent

[maximelegrand]

If I understood pretty well, I'm sure that this is your explications who did the job, I'm not especially good in english but your explain just what needed, and step by step. I thank you again, and I actually share your channel when my mates are in troubles with mathematics, or just to learn things for culture :) . Good luck for the rest.

[cfcalle]

Hey I've been watching your tutorials all day long. Super clear explanations, neat works, and love your voice. Definitely subscribed!

[colinsmith]

Very interesting, thank you. I’ve tried the following problem without success, perhaps you could use it in a future video.
A Christmas tree has a certain base diameter and height (or slant height) Christmas lights of a set length are to be wrapped around the tree equally spaced height wise. If the length of lights is devided into 10 parts, how high up the slant height should each division be. It would make Christmas decorations so much free of stress!
With thanks
Colin Smith

[pamelamartin]

You explain this so clearly and so simply. Thank you for the help!

[kristakingmath]

Awesome!! Thank you so much... I'm soooo impressed with you for being able to understand something so complicated that's explained in a foreign language... amazing! :D

[raspberry]

life saver,  i have a calc test in 2 days and this stomps the teacher's hw answer key

[SeraphimKidd]

I had a homework question exactly like this haunting me. You explained it so well! Thank you!

[anysofiana]

Thanks, you explained it very clear, I like your teaching style

[shoubhikghosh]

A few queries:
1.Is it possible to differentiate the same equation twice and then solve?
2.How do you find out on looking at a question and see if it has to be differentiated once or twice?

[maximelegrand]

I was trying to get something, but I didn't.I was seeing your video, but because I'm french, I was scared about understand something mathematic in english, but finally not! You do such a great job and I thank you for that :) Liked and suscribed!

[racheldavis]

This video just helped me finish maths assignment, thank you so much!

[marilynlucas]

I know this was a very long time ago, but when you solved for height, is the height that you solved for the height of the cone that holds the maximum volume?

[hrshsmpt]

I'm curious about the angle a that was cut out of the circle what would be the optimal angle and how would we find it

[mc]

Hi, amazing video, I was just curious, is there a way to prove that the formula will always yield the maximum volume? It was derived from the formula for the volume of a cone, how do you know this will solve for the maximum volume? Thank you, I hope you can help me!

[CTB]

Great great. May I know what application do you use for this chalk board screen?

[mstuff]

okay so I am doing a homework piece where I calculate the maximum volume of a shape made from an A4 piece of paper I used this but the answer I got was a very large answer I assume the answer I got wasn't squared so would I just square root it to get the answer in 2 dimensions?

[jimmietran]

What if the section is not cut? and the cone is cut to the center which could curl up and could change the height and radius.
How do I find the radius of the maximized volume of a cone? and the max volume of it ? thanks
I don't know if it matters.

[jemcel]

Nice!! But what if I was told to find the dimensions that will yield the max volume? Do I optimize the surface area of the cone?