Visual Sum of Cubes III

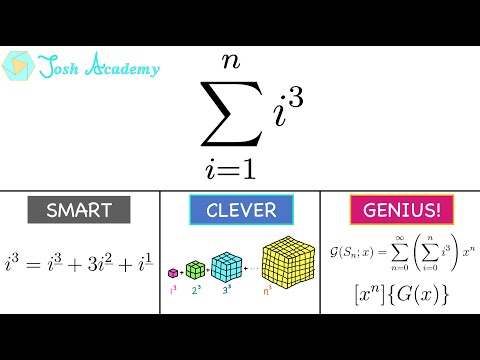
This is a short, animated (wordless) visual proof demonstrating the sum of the first n positive cubes using overlapping gnomons. #mathshorts​ #mathvideo​ #math​ #calculus #mtbos​ #manim​ #animation​ #theorem​ #pww​ #proofwithoutwords​ #visualproof​ #proof​ #iteachmath #finitesums #discretemath #calculus #sum #induction

Here are two other visual proofs of the same fact:

To learn more about animating with manim, check out:

___________________________________________
Music in this video:
Creative Commons Attribution 3.0 Unported License

[spikypichu]

One of the most underrated channels on youtube. I’ll be sure to share!

[piskounov]

Good work, very well made. This channel really deserves wayyy more and im sure it will blow ! Thank you

[keinKlarname]

One of my favorite formulas - and I have never seen it in this way! Any of your videos gives me some new insight. Thanks a lot.

[johnchessant]

woah, the music was well suited for how epic this is

[spikypichu]

One of the most underrated channels out there. I’ll be sure to share!

[Mutual_Information]

damn that's cool, and I had totally forgotten this equation! love it

[TheBasikShow]

Nice! I think this I my favorite one yet.

[mohammedal-haddad]

The overlaps equal the gaps. That was brilliant!

[JGHFunRun]

Very neat proof. I should add that sum of i at the end can also be visually shown to be equal to (n² + n)/2

This can be done by arranging it into a series of progressively smaller rows that looks like a blocky right triangle. This triangle can then be split into one right triangle with both sides of length n and n triangles with both sides of length 1

[mistycremo]

Hopefully my decision to put words here makes a computer send more people here. Hopefully my careful wording is justified by said computer. I loved this awesome video

[justinwatson]

Which software do you use to make your animations?

[scmtuk]

Is it possible to prove the sum of cubes is the square of triangle numbers, purely using algebra?

It is possible to use the triangular formula to prove that the sum of odd numbers is a square, like so:

The triangular formula is usually derived by adding opposite pairs of terms together, to create the equivalent of double the triangular formula.

That is, (1 + n) + (2 + n - 1) + (3 + n - 2) + (4 + n - 3) + .... + (n - 3 + 4) + (n - 2 + 3) + (n - 1 + 2) + (n + 1), which will simplify to n(n+1), therefore, if 2T(n) = n(n+1) then T(n) = n(n+1)/2

If we do a similar thing for odd numbers, and list the sum of odd numbers up to (2n - 1), then add opposite pairs together, we'll get:
(1 + 2n - 1) + (3 + 2n - 3) + (5 + 2n - 5) + (7 + 2n - 7) + .... + (2n - 7 + 7) + (2n - 5 + 5) + (2n - 3 + 3) + (2n - 1 + 1), which will simplify to n(2n), or 2n^2, and since we've added twice the sum of odd numbers, we need to then divide 2n^2 by 2, to get n^2.

But can we do a similar thing with cube numbers to prove that they are the square of triangular numbers, or vice versa?

[saisthuvanthmadiraju]

ow wow I guessed correctly in the first video of summing cubes

[grumpyparsnip]

1:05 why are we waiting to move the squares. Ah! Need to wait for the dramatic turn in the music.