Complex Analysis: Inverse Laplace Transform 1/sqrt(s)

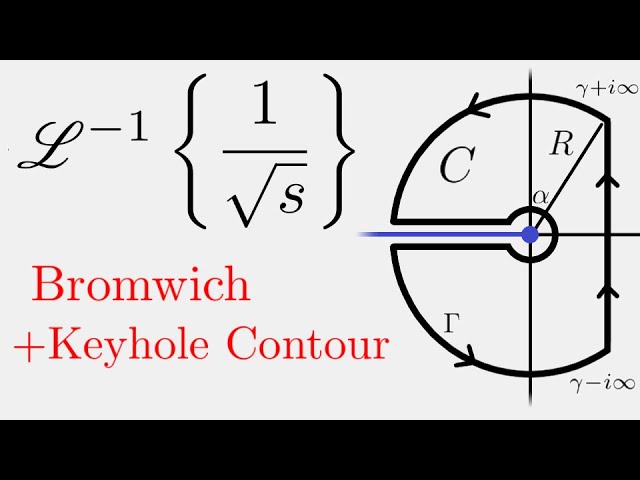
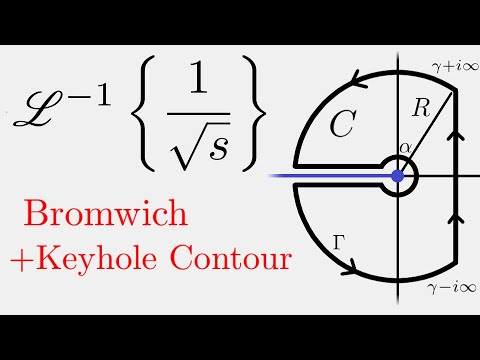
Today, we evaluate the inverse Laplace transform of 1/sqrt(s) using a combination of the Bromwich and keyhole contour.

[Peter_]

It feels pretty amazing to finally see someone actually _calculate_ these things.
This is something that I normally never see - I always see math teachers bring up transform tables. I guess this is because the actual calculations take a very long time, but it is still really cool to see what is going on "behind the scenes" there.

[douglasstrother]

"Applied Complex Variables" by John W. Dettman is a great read: the first part covers the geometry/topology of the complex space from a Mathematicans' perspective, and the second part covers application of complex analysis to differential equations and integral transformations, etc. from a Physicists' perspective. It is a detailed compliment to QN^3 videos.

[Re-lxmd]

When they forgot to give you a laplace table on the exam

[pacolibre]

Does this make 1/sqrt(t) an eigenfunction of the Laplace transform, or does it not count because the input space is different?

[mai]

every video you seem to drag the way to say greetings.

[amnishvachher]

Yeah! Love your lectures. Can you make lectures on the method of steepest descent and also contour integral for bessel or hankel function

[KSMK]

Maybe I didn't understand it very well, why the Psi 1 and Psi 2 don't they cancel here? In the residue theorem proof something like that used to be cancelled

[channalbert]

Wouldn't it be easier to complete the contour as a semicircle-like curve to the right, a kind of D shape, to avoid so many integrals? Thanks for the video!

[zakirreshi]

Could you please solve Integral
x^m/(a^n+x^n), from 0 to infinity
Solution will be like 2pi/[na^(n-1)]* sin[(m+1)pi/n]

[Czeckie]

i dont get why does the integral over omega vanish. Just because it encloses a branch point? I'm rusty in this. But I feel like correct argument should appreciate that the integrand is unbounded, but only because of a factor |ε|^(-1/2) and that is taken care off by multiplying by ε (radius of omega). Is it always guaranteed to work out like that if we have a branch point?

[pollopapas]

In which book can I find the theory and approach used in the video?

[firemaniac]

In Bromwich Contour lemma it is required that the degree of numerator exceeds that from the denominator by at least one. Such doesn't happen for the inverse square root. Am I missing any other lemma?

[hectore.garcia]

May you resolve this integral, Integral of ((x-1)³x)^(1/4) / (x+1)³ from 0 to 1 ? this integral is equal to 3(2⁴)PI/64