filmov
tv
Thomas Barthel - Quantum sim of condensed matter using Trotterized entanglement renormalization
Показать описание
Recorded 08 February 2024. Thomas Barthel of Duke University presents "Quantum simulation of condensed matter using Trotterized entanglement renormalization" at IPAM's Tensor Networks Workshop.
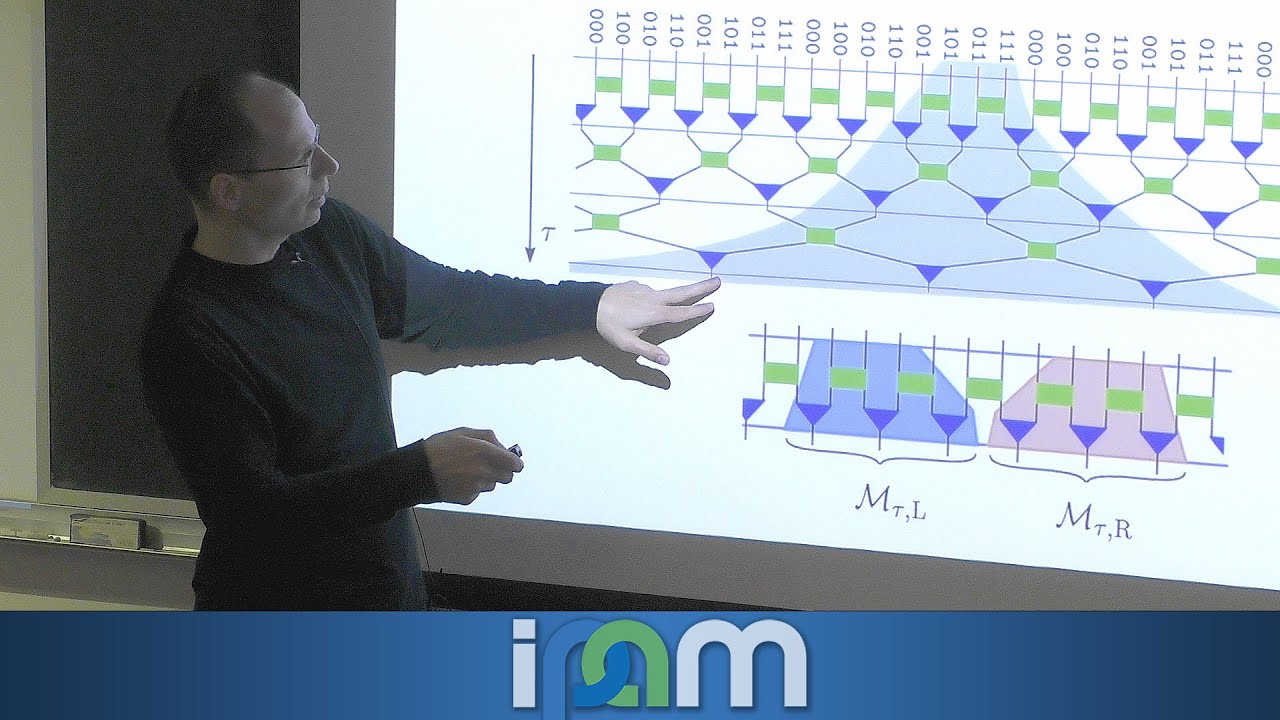
Abstract: I will describe a variational quantum eigensolver for the simulation of strongly-correlated quantum matter based on a multi-scale entanglement renormalization ansatz (MERA) and gradient-based optimization. Due to its narrow causal cone, the algorithm can be implemented on noisy intermediate-scale (NISQ) devices and still describe large systems. The number of required qubits is system-size independent and increases only to a logarithmic scaling when using quantum amplitude estimation to speed up gradient evaluations. Translation invariance can be used to make computation costs square-logarithmic in the system size and describe the thermodynamic limit. For the practical implementation, the MERA disentanglers and isometries are Trotterized, i.e., implemented as brickwall circuits. With a few Trotter steps, one recovers the accuracy of the full MERA. Results of benchmark simulations for various critical spin models establish a quantum advantage, and I will report on first experimental tests on ion-trap devices. For systems with finite-range interactions, one can also show that, in contrast to quantum neural networks, the variational energy optimization of isometric tensor networks like MERA is free of barren plateaus.
Abstract: I will describe a variational quantum eigensolver for the simulation of strongly-correlated quantum matter based on a multi-scale entanglement renormalization ansatz (MERA) and gradient-based optimization. Due to its narrow causal cone, the algorithm can be implemented on noisy intermediate-scale (NISQ) devices and still describe large systems. The number of required qubits is system-size independent and increases only to a logarithmic scaling when using quantum amplitude estimation to speed up gradient evaluations. Translation invariance can be used to make computation costs square-logarithmic in the system size and describe the thermodynamic limit. For the practical implementation, the MERA disentanglers and isometries are Trotterized, i.e., implemented as brickwall circuits. With a few Trotter steps, one recovers the accuracy of the full MERA. Results of benchmark simulations for various critical spin models establish a quantum advantage, and I will report on first experimental tests on ion-trap devices. For systems with finite-range interactions, one can also show that, in contrast to quantum neural networks, the variational energy optimization of isometric tensor networks like MERA is free of barren plateaus.
 0:51:58
0:51:58
 1:09:52
1:09:52
 0:49:16
0:49:16
 0:59:12
0:59:12
 0:23:19
0:23:19
 0:46:48
0:46:48
 0:02:24
0:02:24
 2:17:28
2:17:28
 1:56:07
1:56:07