Prime Ideals (Algebra 1: Lecture 30 Video 4)

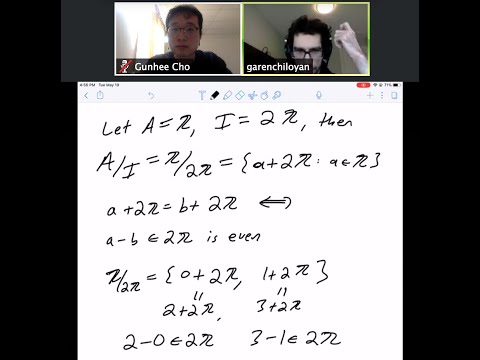
Lecture 30: We started this lecture by first proving that an ideal I in a ring R with unity is all of R if and only if I contains a unit. We then saw that in the case when R is commutative, R is a field if and only if it has no proper non-trivial ideals. We then defined a maximal ideal. We discussed the maximal ideals in Z. We proved that in a ring with identity every proper ideal is contained in a maximal ideal using Zorn's Lemma. We then proved that an ideal M in a commutative ring R with unity is maximal if and only if R/M is a field. We then saw how to use this fact to determine whether certain ideals were maximal. We defined a prime ideal and discussed the maximal ideals in . We saw that an ideal P in a commutative ring R with unity is prime if and only if R/P is an integral domain. As a consequence we saw that in a commutative ring R with unity, maximal ideals are prime. We saw an example of an ideal in Z[x] that is prime but not maximal.

Reading: In this lecture we closely followed the second part of Section 7.4 of Dummit and Foote, starting from Proposition 9 on page 253. We included the definitions that go into Zorn's Lemma from Section 2 of Appendix 1, pages 907-909. It may seem quite surprising at first that something like Zorn's Lemma is really necessary for proofs in algebra, but this is something we will encounter again later in the 206 sequence. It is worth thinking about this argument a little and getting used to what a 'Zorn's Lemma' argument looks like. I highly recommend the blog post 'How to Use Zorn's Lemma' by Tim Gowers.