Angle between radius vector and tangent | module 1 | Calculus #maths #mathguide #teachingmathematics

In this video, we delve into the fascinating relationship between the radius vector and the tangent line to a curve in polar coordinates. We’ll break down complex concepts into manageable steps, making it easier for you to grasp this important topic in calculus and geometry.

🔍 What You’ll Learn:

The components of the polar coordinate system, including the pole, initial line, and key points.
How to derive the angle between the radius vector and the tangent line using polar coordinates.
Detailed calculations involving the tangent slope at a given point, using derivatives and trigonometric identities.
A clear explanation of how to relate polar and Cartesian coordinates.
Whether you’re a student looking to reinforce your understanding or someone interested in the mathematical relationships in polar coordinates, this video is designed for you!

👉 Don’t forget to like, subscribe, and hit the notification bell to stay updated on our latest content!

Feel free to leave your comments or questions below!

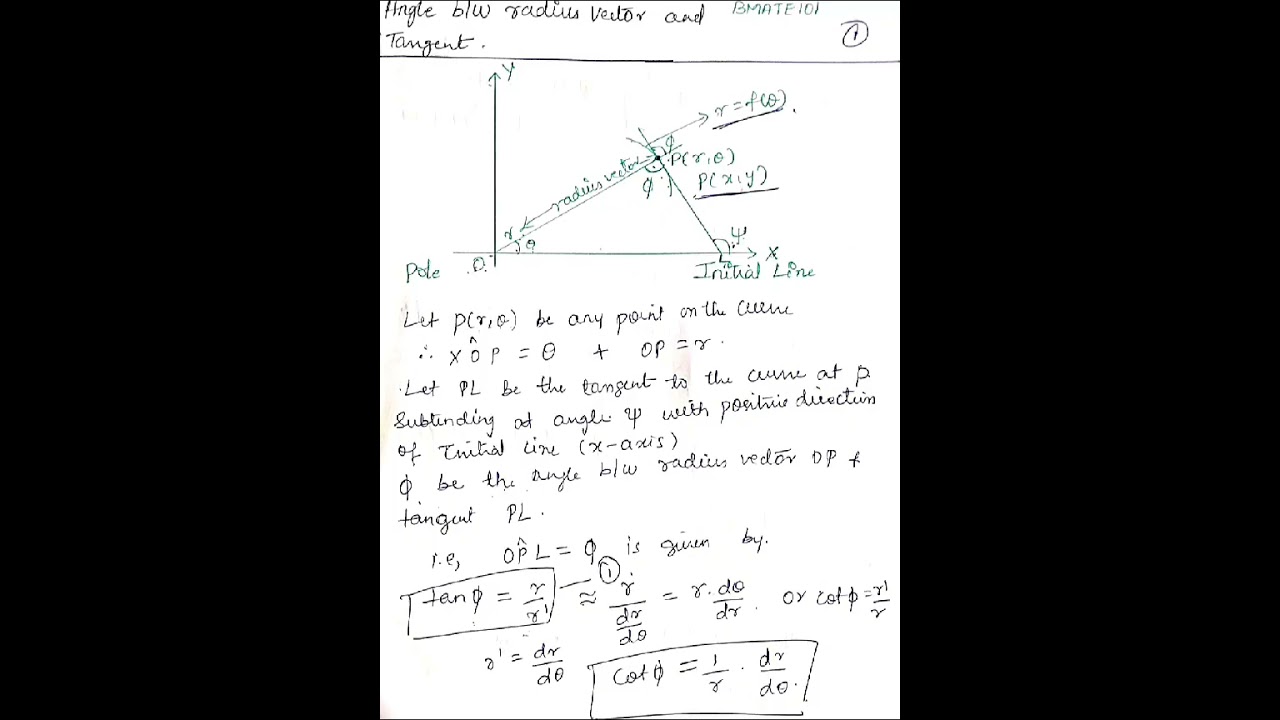
The diagram illustrates the relationship between the radius vector and the tangent line to a curve in polar coordinates.
Components of the diagram:
Pole (O): The origin of the polar coordinate system.
Initial Line: The horizontal axis from which the polar angle is measured.
P(r, θ): A point on the curve, with polar coordinates r and θ.
OP: The radius vector from the pole to the point P.
PL: The tangent line to the curve at point P.
ψ: The angle between the radius vector OP and the tangent line PL.
XOP: The angle θ between the initial line and the radius vector OP.
[Exterior angle = Sum of Interior opposite angles]
ψ = Φ + θ
tanψ = tan(Φ + θ)
tan(A+B) = (tanA + tanB) / (1 - tanA tanB)
tanψ = (tanΦ + tanθ) / (1 - tanΦ tanθ)
Let x, y be the Cartesian coordinates of P.
x = rcosθ, y = rsinθ
r = f(θ)
tanψ = dy/dx ⇒ slope of tangent PL
tanψ = (dy/dθ) / (dx/dθ)
tanψ = (d(rsinθ)/dθ) / (d(rcosθ)/dθ)
tanψ = (r'sinθ + rcosθ) / (r'cosθ - rsinθ)
tanψ = r cosθ + sinθ (dr/dθ)
r(-sinθ) + cosθ (dr/dθ)

where r' = dr/dθ

tanψ = r cosθ + r' sinθ
-r sinθ + r' cosθ

tanψ = r' cosθ / r cosθ + r' sinθ / r cosθ
-r sinθ / r cosθ + r' cosθ / r cosθ

tanψ = r' / r + tanθ
- tanθ + r' / r

tanψ = r' / r + tanθ
1 - r' / r tanθ

tanψ = tanθ + 1 / (1 - tanθ)

Since sinθ / cosθ = tanθ

Comparing eqn ① & ②
-tanɸ = r/ dr/dθ
tanɸ = - dr/dθ
tanɸ = θ(dr/dθ) or cotɸ = -1/(dr/dθ)
Hence Proved