filmov
tv
Solve a! + 5^b = 7^c for integers

Показать описание
Olympiad Math | Solve for (a^5)+(b^5) | Math Olympiad Preparation
Linear equation with one unknown: Solve 5-B=1 step-by-step solution
Step 5 b - How to Solve the Rubik's cube
Learn How to Solve a 5x5 in 8 Minutes (Beginner Tutorial)
Linear equation with one unknown: Solve -14+6b+7-2b=1+5b step-by-step solution
Linear equation with one unknown: Solve (4)/(5)b=12 step-by-step solution
Linear equation with one unknown: Solve 4b+5=1+5b step-by-step solution
Linear equation with one unknown: Solve b/5=2/5 step-by-step solution
Harvard Failed To Solve This | A Challenging Exponential Equation
Linear equation with one unknown: Solve 31=5(b-2) step-by-step solution
Solve (3-√5)/(3+2√5)=a√5-b
Mathematical Olympiad | Solve for a+b | Math Olympiad Preparation
Linear equation with one unknown: Solve -27=-2+5b step-by-step solution
How to Solve a 5x5x5 Rubik's Cube FOR BEGINNERS
Linear equation with one unknown: Solve 5b=35 step-by-step solution
Solve -5(b:1)=8: Linear Equation Video Solution | Tiger Algebra
Linear equation with one unknown: Solve 5b-8=4-b step-by-step solution
Linear equation with one unknown: Solve 2/5b+1=-11 step-by-step solution
Linear equation with one unknown: Solve 11-5b=71 step-by-step solution
Solve 12-b=7-5b: Linear Equation Video Solution | Tiger Algebra
Solve 2(b+1)=5(b-4)+1: Linear Equation Video Solution | Tiger Algebra
Linear equation with one unknown: Solve b+19-5b-7=0 step-by-step solution
Linear equation with one unknown: Solve 8(b-1)=5(b+4)+8 step-by-step solution
Linear equation with one unknown: Solve 2b+8-5b+3=-13+8b-5 step-by-step solution
Комментарии
 0:08:04
0:08:04
 0:01:06
0:01:06
 0:01:24
0:01:24
 0:08:15
0:08:15
 0:01:40
0:01:40
 0:00:58
0:00:58
 0:01:27
0:01:27
 0:00:55
0:00:55
 0:13:35
0:13:35
 0:01:12
0:01:12
 0:05:12
0:05:12
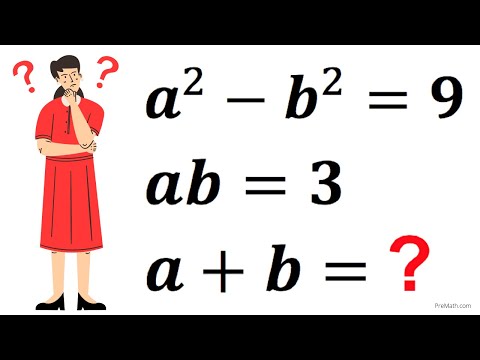 0:08:59
0:08:59
 0:01:14
0:01:14
 0:30:24
0:30:24
 0:00:49
0:00:49
 0:00:58
0:00:58
 0:01:30
0:01:30
 0:01:16
0:01:16
 0:01:22
0:01:22
 0:01:21
0:01:21
 0:02:06
0:02:06
 0:01:26
0:01:26
 0:01:56
0:01:56
 0:01:52
0:01:52