filmov
tv
Griffiths QM Problem 2.2 Solution: Proving that Energy has to be Greater than Potential
Показать описание
In this video I will show you how to solve problem 2.2 as it appears in the 3rd edition of griffiths introduction to quantum mechanics. The problem states:
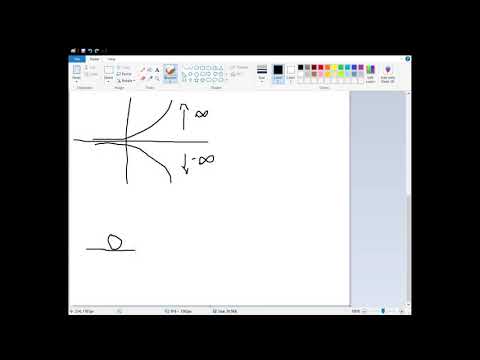
Show that E must exceed the minimum value of the potential for every normalizable solution ot the time-independent Schrödinger equation. What is the classical analog to this statement?
If you enjoy my content, please consider checking out my Patreon!
Also, consider subscribing and following me on my socials!
My name is Nick Heumann, I am a recently graduated physicist. I love to teach physics, so I decided to give YouTube a try. English is not my first language, but I hope that you can understand me well enough regardless.
▬ Contents of this video ▬▬▬▬▬▬▬▬▬▬
00:00 Introducing the problem
00:20 Proof
05:01 Please support my patreon!
Show that E must exceed the minimum value of the potential for every normalizable solution ot the time-independent Schrödinger equation. What is the classical analog to this statement?
If you enjoy my content, please consider checking out my Patreon!
Also, consider subscribing and following me on my socials!
My name is Nick Heumann, I am a recently graduated physicist. I love to teach physics, so I decided to give YouTube a try. English is not my first language, but I hope that you can understand me well enough regardless.
▬ Contents of this video ▬▬▬▬▬▬▬▬▬▬
00:00 Introducing the problem
00:20 Proof
05:01 Please support my patreon!
0:05:12
Griffiths QM Problem 2.2 Solution: Proving that Energy has to be Greater than Potential
0:05:34
Griffiths QM Problem 2.2
0:04:02
Griffiths Quantum Mechanics 3rd Ed. | Problem 2.2
0:22:49
Griffiths intro to quantum mechanics problem 2.2 solution
0:26:59
SOLUTION to Griffiths QM problem 6.19 (3rd edition) /6.21 (2nd edition): Zeeman effect for n=2
0:45:56
Griffiths QM 2.27 Solution: Finding Transmission coefficient for double delta potential
0:25:46
Step-by-Step Solutions to Griffiths Quantum Mechanics Problems 2.1 to 2.4
0:15:31
Griffith Quantum Mechanics Solution 1.5: Normalization, Expectation Values, and Standard Deviation
0:26:23
Griffiths QM 2.33 Solution: Transmission and reflection Coefficient for Step Potential Barrier
0:06:11
Griffiths Quantum Mechanics 3rd Ed. | Problem 2.5(a)
0:10:50
Griffiths Introduction to Quantum Mechanics Solution 7.2: Harmonic Oscillator Perturbation Theory
0:23:15
Griffiths QM 2.1 (3rd ed) Solution: Proving Three Important Theorems
0:08:34
Griffiths Quantum Mechanics 3rd Ed. | Problem 2.10(a)
0:03:44
Griffiths Quantum Mechanics 3rd Ed. | Problem 2.5(e)
0:17:32
Griffiths QM 1.6 Solution: Expectation Values For Gaussian Distribution (rho(x)=Ae^(-lambda(x-a)^2)
0:08:26
Griffiths Quantum Mechanics 3rd Ed. | Problem 2.5(b)
0:07:06
Griffith Quantum Mechanics Solutions 1.1
0:56:04
Griffiths QM Problem 8.12 Solution: Try this VERY hard WKB Problem with TOUGH Integrals!
0:05:16
Griffiths Quantum Mechanics 3rd Ed. | Problem 2.7 (c) and (d)
0:03:46
Griffiths QM Problem 1.6
0:05:14
Griffiths Quantum Mechanics 3rd Ed. | Problem 2.9
0:29:10
Griffiths QM Problem 2.5: Expectation values and Uncertainty Principle for Infinite Square Well
0:25:26
Griffiths quantum mechanics problem 2.9 solution
0:02:02
Griffiths Quantum Mechanics 3rd Ed. | Problem 2.5(d)
Комментарии