filmov
tv
Solving An Infinite Exponential Equation
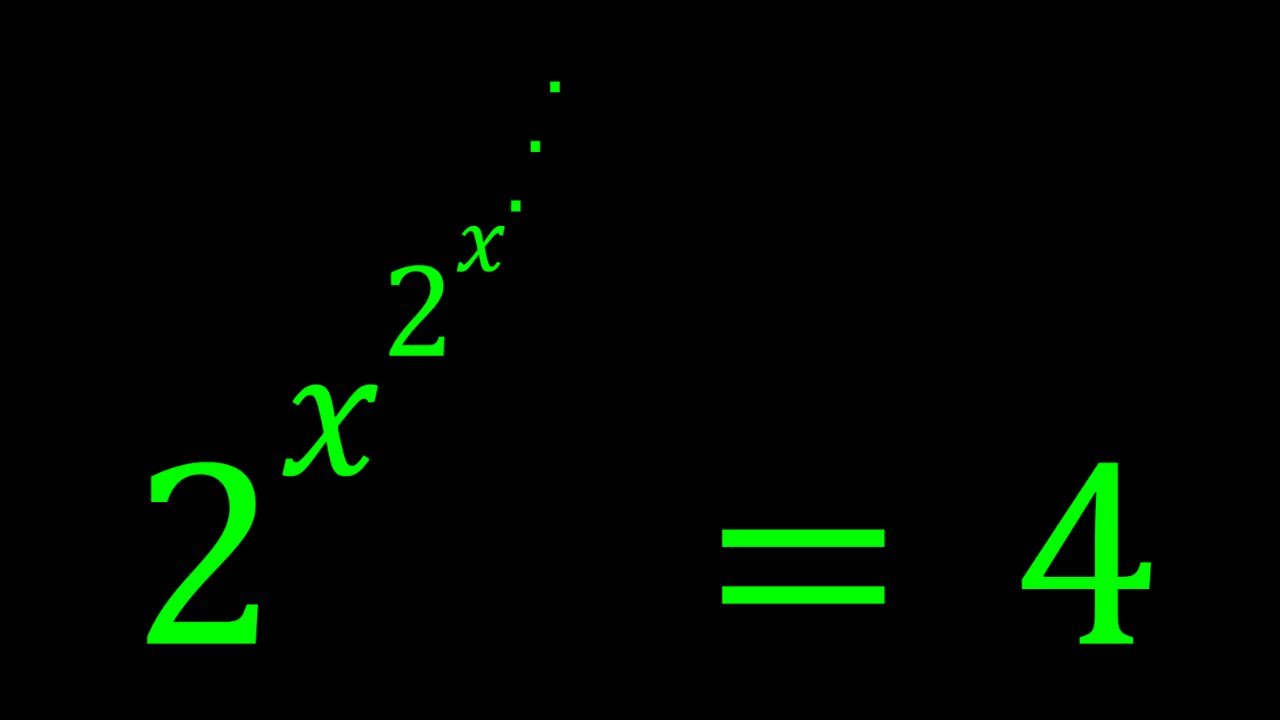
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ExponentialEquations #Exponentials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ExponentialEquations #Exponentials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Solving An Infinite Exponential Equation
an infinite exponential equation
Solving a Super Exponential Equation
An infinite Exponential Radical Equation
Algebra Math Problem | Solve the Exponential Equation x^x^x^x.. (infinite times) = 2 #shorts
How to Graph Exponential Functions
Can You Solve This Exponential Equation? | Algebra Math Problem With Solution
Challenge Exponential Equation 8^x=2^(y-3) with Infinite Solutions Solve by Logarithms
Absolute Value and sign changes.
Solving Infinite Exponential Equation
A Quick and Easy Exponential Equation
5 simple unsolvable equations
How to Solve an Exponential equation – A Step-by-Step Guide
Solving An Exponential Equation for All Solutions
exponential function | infinite series #calculus #math #animation #learn #study
Solving the Exponential Equation (1/2)^(3x - 6) = 8^(x + 1)
Solving a Nice Exponential Equation in Two Ways
An Infinite Radical | Algebra Challenge
A Somewhat Exponential Equation Solved in Two Ways
A Very Interesting Exponential Equation | 1ˣ = -1
Exponential Form to Logarithmic Form #Shorts #algebra #math #maths #mathematics #lesson #howto
Solving An Exponential System
Limits at Infinity of Exponential Functions | How to find limits at infinity | Calculus - Part 4
Logarithmic Form to Exponential Form (Natural Log Edition) 🤯 #Shorts #algebra #math #education
Комментарии
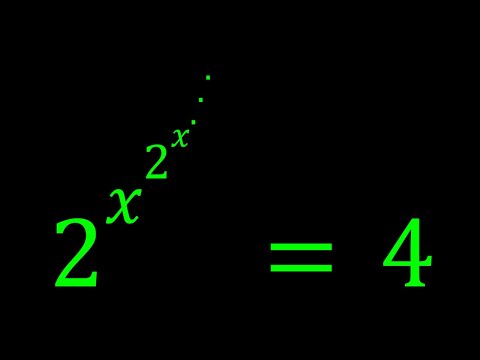 0:05:50
0:05:50
 0:01:19
0:01:19
 0:06:26
0:06:26
 0:10:54
0:10:54
 0:00:34
0:00:34
 0:00:40
0:00:40
 0:02:37
0:02:37
 0:05:09
0:05:09
 0:36:06
0:36:06
 0:00:30
0:00:30
 0:04:28
0:04:28
 0:00:50
0:00:50
 0:11:59
0:11:59
 0:08:48
0:08:48
 0:00:12
0:00:12
 0:02:24
0:02:24
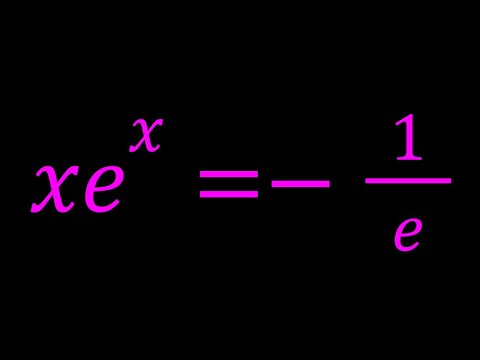 0:11:14
0:11:14
 0:00:39
0:00:39
 0:08:52
0:08:52
 0:01:00
0:01:00
 0:00:22
0:00:22
 0:00:37
0:00:37
 0:16:35
0:16:35
 0:00:28
0:00:28