Lie Groups and Lie Algebras: Lesson 11 - The Classical Groups Part IX

preview_player
Показать описание
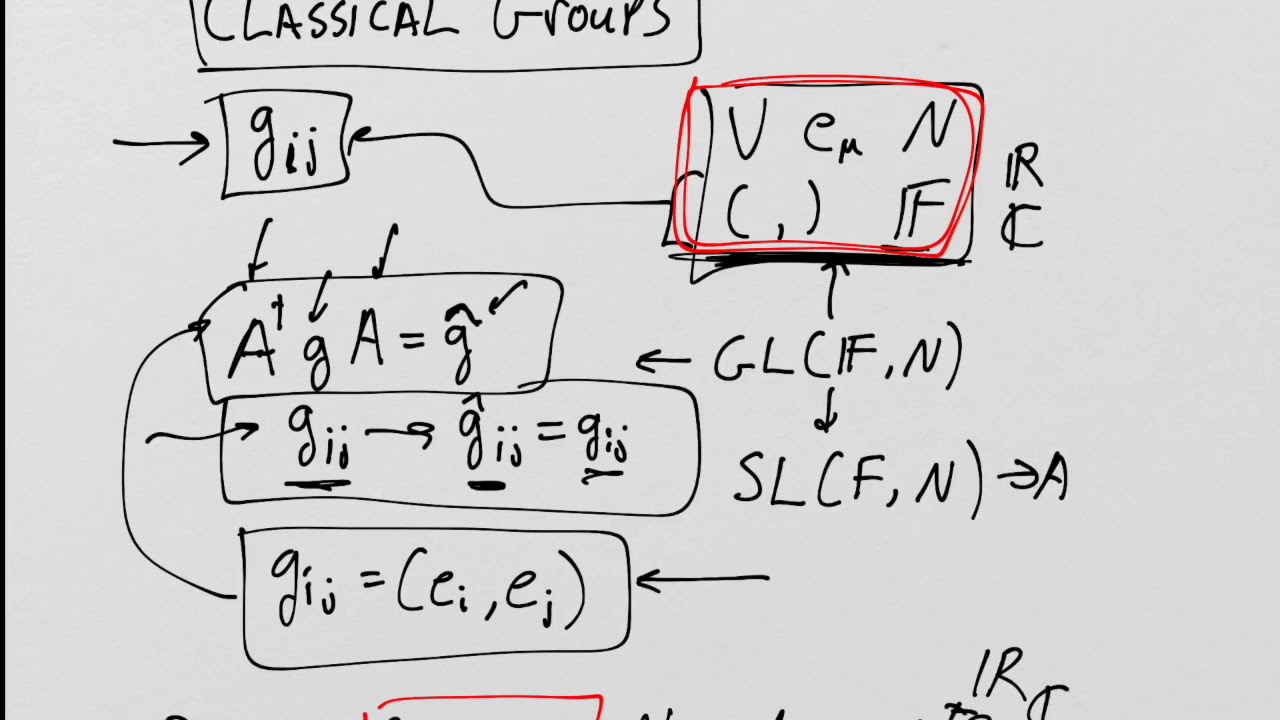
Lie Groups and Lie Algebras: Lesson 11 - The Classical Groups Part IX

In this lecture we count the degrees of freedom for the classical groups.

Please consider supporting this channel via Patreon:

  1. XylyXylyX
  2. Lie Groups
  3. Lie Algebra
Рекомендации по теме
Why study Lie 0:04:26

Why study Lie theory? | Lie groups, algebras, brackets #1

What is Lie 0:21:57

What is Lie theory? Here is the big picture. | Lie groups, algebras, brackets #3

Spinors for Beginners 0:36:23

Spinors for Beginners 16: Lie Groups and Lie Algebras

Lie groups and 1:43:12

Lie groups and their Lie algebras - Lec 13 - Frederic Schuller

Lie Groups and 0:03:11

Lie Groups and Lie Algebras

Representation theory of 1:32:39

Representation theory of Lie groups and Lie algebras - Lec 17 - Frederic Schuller

Lie algebras visualized: 0:44:31

Lie algebras visualized: why are they defined like that? Why Jacobi identity?

Lie groups: Introduction 0:36:14

Lie groups: Introduction

An introduction to 2:42:45

An introduction to Algebraic Groups and the Theory of Invariants. Lecture 2. Zhgun V.S.

Lie Algebras and 1:00:59

Lie Algebras and Homotopy Theory - Jacob Lurie

Lie group and 0:00:59

Lie group and Lie algebra visual simulation on a complex manifold.

Lie groups: Lie 0:36:29

Lie groups: Lie groups and Lie algebras

Lie Groups and 0:50:56

Lie Groups and Lie Algebras: Lesson 34 -Introduction to Homotopy

Lie algebras with 0:52:40

Lie algebras with @TomRocksMaths

Lie Algebras 1 0:27:32

Lie Algebras 1 -- Definition and basic examples.

An Introduction to 1:01:08

An Introduction to Lie Groups and Algebras - I.

Lie algebra Lie 0:30:42

Lie algebra Lie group dictionary

Lie groups: Lie 0:30:53

Lie groups: Lie algebras

Lie Groups and 0:52:20

Lie Groups and Lie Algebras: Lesson 39 - The Universal Covering Group

Lie Groups and 0:45:17

Lie Groups and Lie Algebras: Lesson 35 - The Fundamental Group

Lie groups 1 0:02:50

Lie groups 1 - manifolds

Lie Groups and 0:44:18

Lie Groups and Lie Algebras: Lesson 26: Review!

You don't need 0:00:40

You don't need to be afraid of Lie algebras!

[Lie Groups and 1:11:50

[Lie Groups and Lie Algebras] Lecture 15. Basics of root systems

Комментарии
Автор

Between 31:27 and 31.50, you seem to confuse the *symmetry between the elements* (symmetric/anti-symmetric ) with the *functional form of the metric* (bilinear or sesquilinear). An an example: bilinear means that (αeₖ, eₗ) = gₖₗ α and symmetric means gₖₗ = gₗₖ. For info only for all: I rewrote the table as follows (where * means the transposed value ).
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
- - - -
bilinear sesquilinear
(α eₖ, eₗ) = gₖₗ α (α eₖ, eₗ) = (gₖₗ)*α*
- - - - - - - -- - - - - - - - - - - - - - - - - - - - -
- - -
symmetric: gₖₗ = gₗₖ and F=R O(N₊, N₋; F) ---
hermetian: gₖₗ = (gₗₖ)* and F=C, Q O(N₊, N₋; F) U(N₊, N₋ ; F)
anti-symmetric: gₖₗ = - gₗₖ and F=R, C, Q Sp(2N; F) ---
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
- - - - - - - - - - -
I also defined three types of symmetry: symmetric, hermetian and anti-symmetric (this also explains the difference in notation: Gilmore uses the word symmetric for all F=R, C, Q while you uses the word symmetric when F=R and the word hermetian when F=C, Q).

jacquessmeets
Автор

Your matrix example at around 15:40 is not right. The displayed matrix shoul have 0 diagonal . In fact, symplectic matrices have pairs of +1, -1 around a 0 diagonal

antoniomranz