filmov
tv
Spinors for Beginners 16: Lie Groups and Lie Algebras

Показать описание
Videos on momentum operator generating translations in quantum mechanics:
0:00 - Introduction
2:45 - Groups & Lie Groups
4:00 - Exponent of a so(3) Matrix
7:40 - Calculating so(3) generators
9:50 - Momentum generators translations
10:58 - so(3) traceless proof
13:35 - so(3) anti-symmetric proof
15:11 - Warning about matrix exponentials
16:43 - Lie Algebra Bracket
20:24 - Structure coefficients
21:48 - Lie Algebras as Tangent Spaces
23:30 - Lie Algebra Property Proofs
30:15 - Summary of so(3)
31:05 - Overview of so+(1,3)
32:50 - Spin-1 and Spin-1/2 representations
34:40 - Math vs Physics conventions
Spinors for Beginners 16: Lie Groups and Lie Algebras
Spinors for Beginners 17: The spin 1/2 representations of SU(2) and SL(2,C)
Spinors for Beginners 20: Lorentz Group / Algebra Representation Theory
Spinors for Beginners 19: Tensor Product Representations of su(2) [Clebsch-Gordan coefficients]
Spinors for Beginners 2: Jones Vectors and Light Polarization
Spinors for Beginners 6.1 - Equivalence of Quaternions, Sigma Matrices, and SU(2)
Spinors for Beginners 3: Polarizations and SU(2) Matrices [and O(3), SO(3), U(2)]
Why study Lie theory? | Lie groups, algebras, brackets #1
[Lie Groups and Lie Algebras] Lecture 16. Bases and Weyl chambers
Spinors for Beginners 12: How the Spin Group Generalizes Quaternions to any Dimension
Lie groups
Custom Ice Rod Revolution - In-Depth Outdoors TV - Season 6, Episode 3
Spinor Fields and the Dirac Lagrangian
Lie Groups and Lie Algebras: Lesson 25 - the commutator and the Lie Algebra
The Lie group SL(2,C) and its Lie algebra sl(2,C) - lec 15 - Frederic Schuller
Symmetric Physics | How Do Spinors Transform?
Period on the road 😱 | Omg..
U(N) Intertwiners, Part 3 - U(N) Lie Algebra, Spinor Formulation of LQG, May 30, 2021
Michael Atiyah, What is a Spinor
Daiwa Spinning for Saltwater 2017
Particle Physics Lecture 8: Spinors II
Strange Math Books That Will Make You Wonder
I Segreti delle MATRICI di PAULI
Math Methods in Physics Lecture 27: I Won't Lie, This One Is The Best
Комментарии
 0:36:23
0:36:23
 0:38:19
0:38:19
 0:53:40
0:53:40
 0:40:00
0:40:00
 0:17:52
0:17:52
 0:14:20
0:14:20
 0:24:16
0:24:16
 0:04:26
0:04:26
 1:08:53
1:08:53
 0:47:16
0:47:16
 0:05:39
0:05:39
 0:28:01
0:28:01
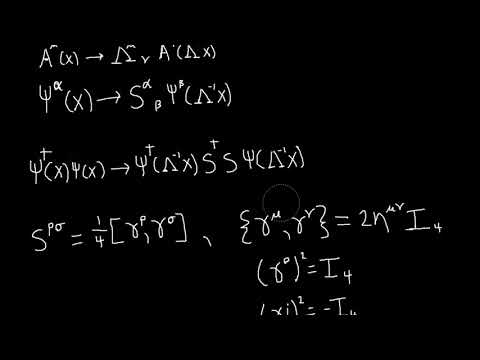 0:07:27
0:07:27
 0:49:52
0:49:52
 1:51:13
1:51:13
 0:23:16
0:23:16
 0:00:41
0:00:41
 1:33:40
1:33:40
 0:38:23
0:38:23
 0:16:28
0:16:28
 0:57:01
0:57:01
 0:12:29
0:12:29
 0:25:25
0:25:25
 1:26:18
1:26:18