Ellipses in Perspective

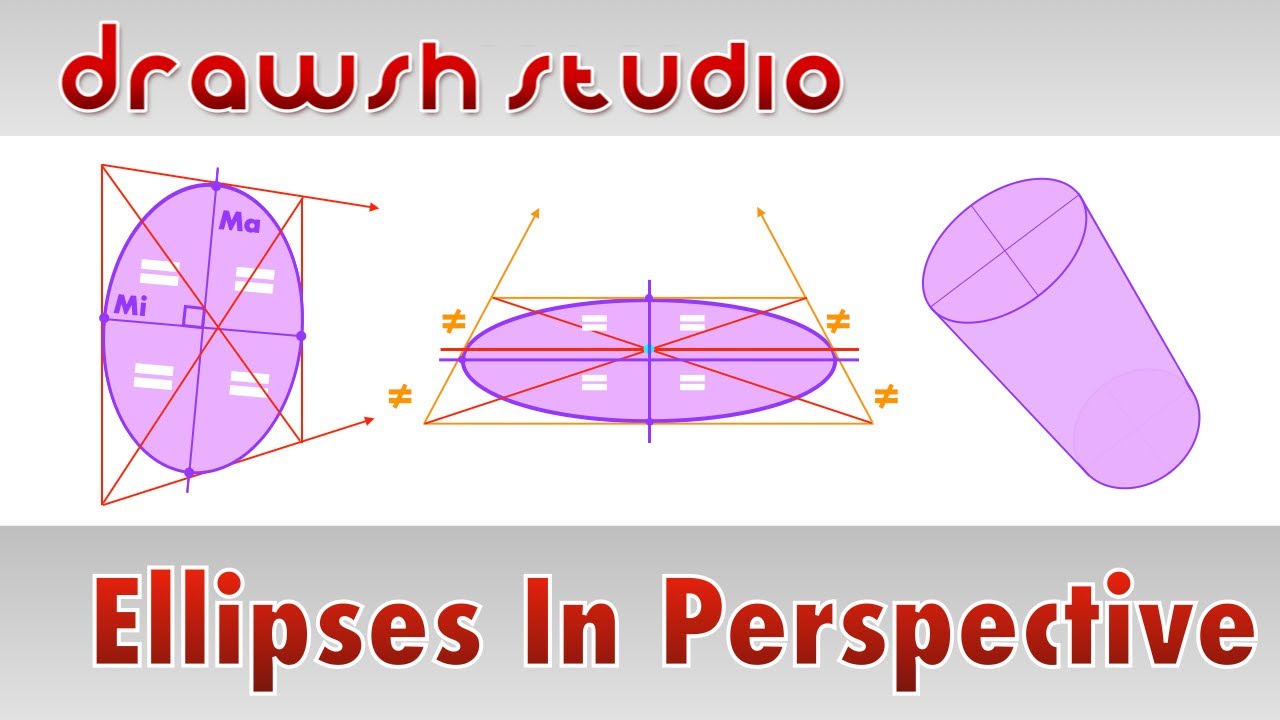
This video teaches you the rules that guide drawing ellipses in perspective. Ellipses are one of the most complicated topics in perspective, but this video will take you through the principles of ellipses in a straightforward and clear way. This is part 1 of 2 ellipse videos, the next will give step by step instructions on how to construct ellipse in perspective.

Find Drawsh Studio on:
Instagram @drawshstudio

[Jobiventure]

You gave us a whole free well-edited schooling 😭😭😭! How am I supposed to thank you 😭 !

[illustratornamedkasper]

This is by far the best and clearest explanation of ellipses in perspective I've seen in here. Thanks!

[tubr]

Nice discussion. A few observations:
- 1:36 not a rectangle but a square around the circle in perspective (if you are talking about the result it's not a rectangle but a trapezoid)
- 3:26 the assertion "because the minor axis is perpendicular to the plane of the ellipse, it will cross the even mathematical center of the ellipse" is inaccurate. It should say "because the minor axis of the ellipse coincides with the axis of the cylinder of the original circle (i.e. perpendicular to the plane of the circle AND goes through the center of the circle), it will cross the even mathematical center of the circle and the square.
center of the ellipse"
- 3:38 (this is a major issue) when a horizontal circle inscribed in a square is drawn in 1PP off center, the tangents of the circle should touch the sides of the original square, so that the lines through those tangents converge into the same VP or be parallel to the horizon. Since this doesn't happen here, it's not a true circle in perspective (1:12), but simply an ellipse inscribed in a perspective trapezoid of the square.

The problem is that you can't use a straight ellipse to show a perspective circle in 1PP off center. It must be a *skewed* ellipse. (Not simply rotated as alluded at 3:44)

In 1PP the coincidence of the minor axis and the cylinder axis should hold, but the major axis would no longer be perpendicular to the minor axis.
It is the same kind of transform used in Tilt Shift Lenses to compensate for vertical line convergence. Basically adjusting a 3PP to 2PP or 1PP.

In this video in the 2PP there is no ellipse distortion because the object is crossing the horizon line. When dropped away from the horizon (2-3 times the size), the ellipse distortion will again be present (by minor and major axes being not perpendicular).

[VitaMiracolosa]

This is the best and clearest explanation ever! Thank you!

[niesoire]

Man, I’ve watched so many vids on ellipses in perspective, and they all left me confused. This one? Game changer. Finally makes sense. You’re a legend!

[niesoire]

Man, I’ve watched so many vids on ellipses in perspective, and they all left me confused. This one? Game changer. Finally makes sense. You’re a legend!”

[hak]

It's a crime that this video has so few views! This single 7 minutes and 32 seconds video solve a lot of problem you will have with ellipses in perspective than you could imagine! Thank you so much for your video, hope that more people will find out this amazing video.

[MrMoto]

This is a nice introduction to perspective drawing, but the animation following 3:40 is misleading. The reason the tilted ellipses don't "feel right to our eyes" is because they were tilted the wrong way! Assuming they are to represent circles on the ground plane, then the minor axes should be tilted very slightly away from the centre of vision, not toward it.

[art]

I don't know what to say! This is what I have been looking for so long! I never ever could think that minor axis goes from vanishing point and that parts of ellipse always should be perpendicular to each other! That`s amazing!

[chenyz]

This is the best and clearest explanation I've ever seen! Thank you!

[dairic]

After five years of drawing I finally understand ellipses! Thanks!

[BonfaLuiz]

Can you please clarify a couple of things:

@ 3:16
"Minor axis needs to be perpendicular to the plane of the ellipse"
But minor axis (as well as major axis) is IN the plane of the ellipse and it can't be perpendicular to it. (A plane is a flat surface on which the ellipse is drawn).

@ 4:03 "Because the plane of the ellipse will be angled to our view we have to account for the ellipse to be slightly tipped in space".
Does that simply mean that the ellipse in this case should be just drawn slanted to look better (more natural)?

[hlaefdige]

Ich habe eingige Videos zum Thema Ellipse und Perspektive gesehen, dies hier ist das absolut verständigste - Vielen Dank!

[lionssin]

Insanely well done educational video. I've struggled with vague descriptions of how to draw ellipses from almost every other video except this one, ty

[yearsago]

At 3:31 the ellipses on the left and right are placed slightly incorrectly. A circle must touch the middle of the 4 sides of the squares, but the ellipses (circles in perspective) are not doing it in the video. You should rotate the minor axes slightly to reach their correct position if i'm not wrong. Please correct me if I am.

[shymaniac]

Can I have a question to the 3:32 moment? If we assume that these ellipses on a left and a right side are perfect cirlces in perspective, then they must be inscribed into squares. Doesn't that mean that the ellipses should be slanted a bit so they would touch the centres of the squares' sides (in the points where red lines cross the sides of the squares), becasue circles inscribed into squares do so? That even happens when you show us an ellipse standing up example. You tipped the ellipse a bit so it could fit into a square in perspective correctly.

[anandartwork]

This is by far the best video on ellipses! You've earned more than my subscription! <3

[Tha_Pencil]

You make better videos than even proko! Amazing! Thank you so much!

[thorliebhammer]

This is the gem I've been dreaming of for quite some time

[sumitshrestha]

Had to watch 3 times to get the paradox in my head😅. Anyway these videos are top-notch, i appreciate these videos, please keep em' coming sirr!