filmov
tv
Taking the Inverse Fourier Transform of the Fourier Transform
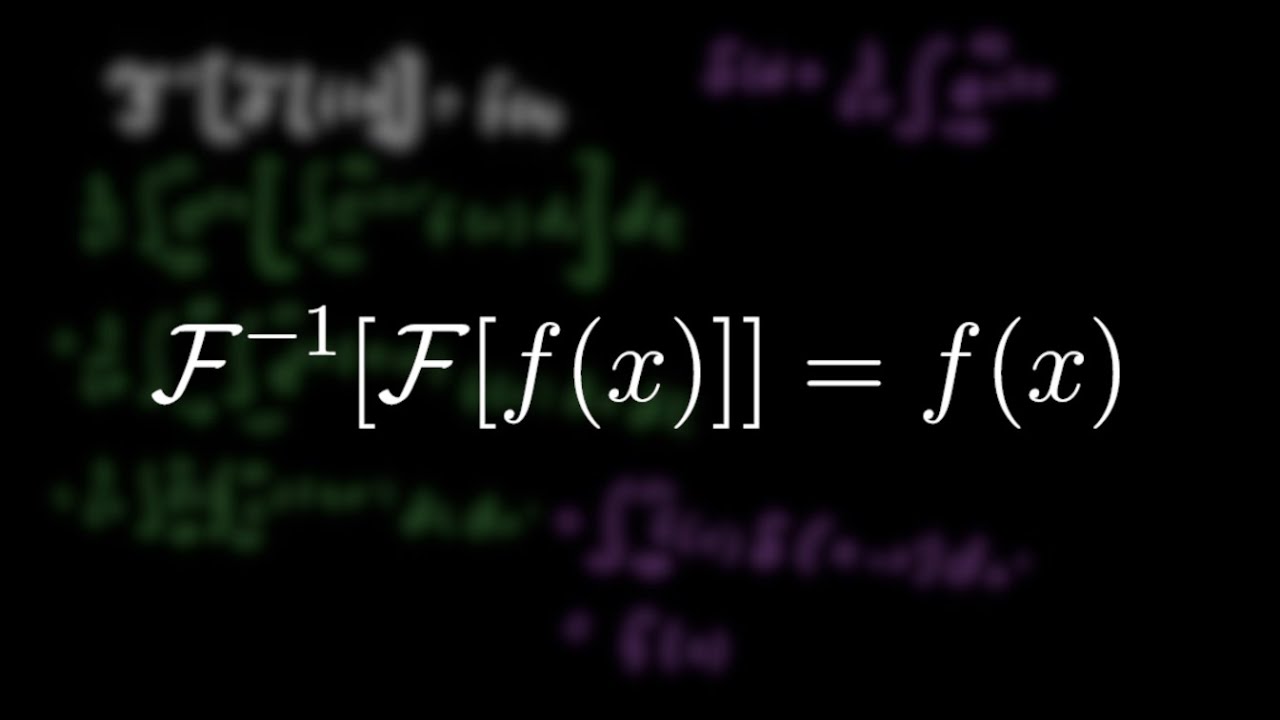
Показать описание
In this video I show that you really do get the identity back when you take the Inverse Fourier transform of the Fourier transform.
To see how you derive the delta function integral representation, visit:
For more videos in this series, visit:
To see how you derive the delta function integral representation, visit:
For more videos in this series, visit:
The inverse Fourier transform
Signals and Systems - Inverse Fourier Transform
Taking the Inverse Fourier Transform of the Fourier Transform
What is the Inverse Fourier Transform?
Fourier Transform and Inverse Fourier Transform: What's the difference?
But what is the Fourier Transform? A visual introduction.
Inverse Fourier Transform Problem Example
Can you guess the song? Fourier Music Decomposition
Proof of inverse Fourier transform
Fourier Transform Equation Explained ('Best explanation of the Fourier Transform on all of YouT...
Inverse Fourier Transform Solved Examples in Signals and Systems
Restoring a picture using the FOURIER TRANSFORM! #VeritasiumContest
Inverse Fourier Transform Problem Example 3
The inverse Fourier transform - example
Inverse Discrete Time Fourier Transform (IDTFT) explained visually
Inverse Fourier Transform of 1/(1+jw)^2
UConn HKN - Signals and Systems - Inverse Fourier Transform
Why do we use the Fourier Transform?
Inverse Fourier transform
Signals and Systems- Inverse Fourier Transform - Introduction
Calculus using MATLAB 31 - Inverse Fourier Transform
Fourier Transform Examples and Solutions | Inverse Fourier Transform
Signals & Systems - Inverse Fourier Transforms - working examples - 2
Fourier cosine transform @MathsNStats #statistics
Комментарии
 0:06:52
0:06:52
 0:06:58
0:06:58
 0:04:42
0:04:42
 0:00:59
0:00:59
 0:12:33
0:12:33
 0:20:57
0:20:57
 0:09:47
0:09:47
 0:03:58
0:03:58
 0:18:02
0:18:02
 0:06:26
0:06:26
 0:12:18
0:12:18
 0:01:00
0:01:00
 0:05:42
0:05:42
 0:11:14
0:11:14
 0:09:02
0:09:02
 0:07:32
0:07:32
 0:07:30
0:07:30
 0:00:59
0:00:59
 0:08:52
0:08:52
 0:17:22
0:17:22
 0:01:20
0:01:20
 0:27:33
0:27:33
 0:10:34
0:10:34
 0:00:05
0:00:05