Rigid Body Rotation - Kinetic Energy and Moment of Inertia

A rigid body is a body whose particles remain at the same relative positions to each other.
We look at a body in outer space (no gravity) which is free to rotate about a smooth axle.
When an external force is applied, the body has an angular acceleration about the axle (analogous to Newton 2)
When this force is removed, the body rotates with constant angular speed w about the axle forever (analogous to Newton 1).
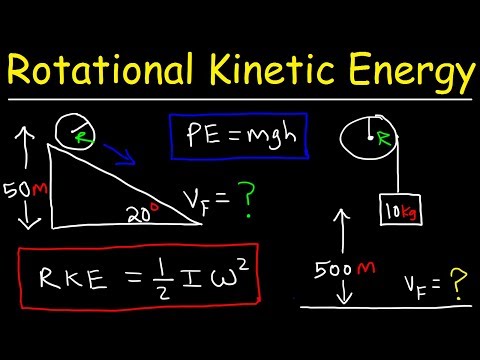
The (rotational) kinetic energy of the body is the sum of the kinetic energies of the particles of the body. This is 1/2*I*w^2 (analogous to 1/2 *m*v^2 for a particle) where I is the moment of inertia of the body about the axle.
I depends on the mass of the body and the distribution of this mass about the axle.
I is a measure of the body's resistance to angular acceleration in the analogous way that m is a measure of a particle's resistance to acceleration.