filmov
tv
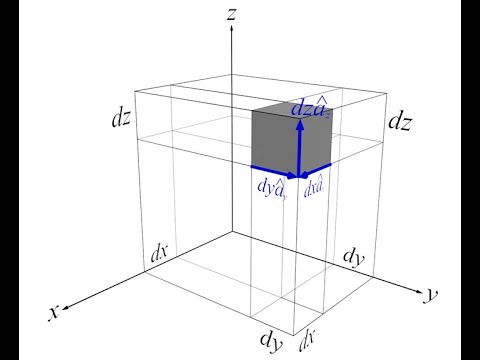
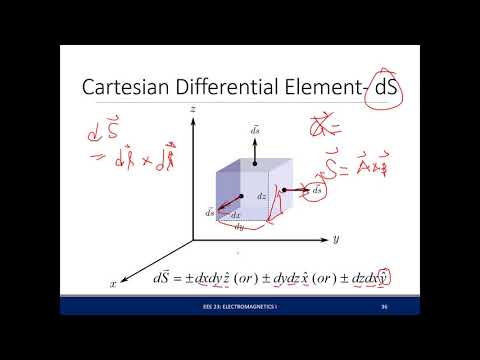
Differential elements dL, dS, dV in rectangular, cylindrical and spherical systems
Показать описание
This video is about how to visualize and how to find the differential elements such as small length dL, small area element dS and small volume element dV for Cartesian (rectangular), Cylindrical and Spherical Systems. This topic is important in the build up for Stokes Theorem , Divergence Theorem and other vector related topics and Engineering subjects like Electromagnetic field theory. This will prove helpful in engineering exams like GATE and IES.
Often students don't know what to do of dL, dS or dV elements they encounter in line integral, Surface (double) integral, volume (triple) integral.
This video takes a basic view and basic understanding of all the differential elements.
Please subscribe and share as much as possible!
.
JOIN Ed Sharpener to get access to perks:
If you are a GATE aspirant, or preparing for any other competitive exam and need a test-series which is value for your money, buy a testbook pass at greatly discounted prices.
Study Smart with thousands of Mock Tests for RRB, SSC & hundreds of Government Exams with Testbook Pass.
Use Coupon Code " EDS10" to avail the discount.
Often students don't know what to do of dL, dS or dV elements they encounter in line integral, Surface (double) integral, volume (triple) integral.
This video takes a basic view and basic understanding of all the differential elements.
Please subscribe and share as much as possible!
.
JOIN Ed Sharpener to get access to perks:
If you are a GATE aspirant, or preparing for any other competitive exam and need a test-series which is value for your money, buy a testbook pass at greatly discounted prices.
Study Smart with thousands of Mock Tests for RRB, SSC & hundreds of Government Exams with Testbook Pass.
Use Coupon Code " EDS10" to avail the discount.
0:24:58
Differential elements dL, dS, dV in rectangular, cylindrical and spherical systems
0:06:09
Volume Elements (dV) in Cartesian, Spherical, and Cylindrical Coordinates
0:04:20
Lec 4-Differential Elements dI,dS,dV in Co ordinate Systems,Electromagnetic fields Theory
0:04:09
Physics Ch 67.1 Advanced E&M: Review Vectors (76 of 113) Area Element in Spherical Coordinates
0:03:39
5. Differential elements for each coordinate system
0:40:21
Cordinates and differential elements
0:02:40
Physics - Advanced E&M: Ch 1 Math Concepts (26 of 55) Cylindrical Coordinates:Area & Volume ...
0:06:19
Deriving the Differential Area Element in Polar Coordinates
0:20:17
Electromagnetic Theory #3 - Basics of Cylindrical Coordinate System - dl, dS, dV
0:15:25
Lecture -- Differential Length Area & Volume
0:10:01
Electromagnetic Theory #2 - Basics of Cartesian Coordinate System - dl, dS, dV
0:08:14
4.1 Multiple Integration - #28 Finding dV in Spherical Coordinates
0:05:14
Understanding dV in cylindrical coordinates
0:18:48
Differential elements in Cylindrical Coordinate system || Differential length, surface and volume
0:19:35
Electromagnetic Theory #4 - Basics of Spherical Coordinate System - dl, dS, dV
0:21:17
Differential elements in cartesian coordinate system || Differential Length, Surface and Volume
0:44:36
L5: GRADIENT OF A SCALAR BY USING DIFFERENTIAL ELEMENTS.
0:10:54
Spherical Coordinates Differential Element (MC-63)
0:30:11
Electromagnetics - Differential Vectors
0:11:58
Differential length in Cartesian Co-ordinate system
0:05:47
What is a Differential Line Element?
0:16:12
Electromagnetics | Vector Calculus | Differential Elements and Integrals (Line, surface and volume)
0:01:44
Difference Between Partial and Total Derivative
0:50:55
Vector Calculus Part 1 - Calculations Involving Differential Length, Surface and Volume
Комментарии