Скалярное произведение векторов.

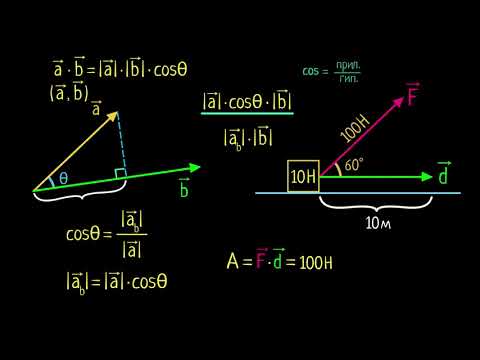
Операция над двумя векторами, результатом которой является число , не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними

[DDsWth]

Даже спустя 5 лет после того, как вы сняли видеоролик он помогает людям, спасибо Вам большое!

[ЯрославМельничук-ьц]

Найкраще пояснення яке є на всьому Ютубі 👍

[justforresearch]

Спасибо большое за ваши видео! Один из немногих каналов, где можно найти доходчивое объяснение вывода формул. Спасибо!!!!

[gnot]

Такие не сложные факты а 90% школ об этом не говорят. Спасибо вам

[ПетроваВероника-ми]

Спасибо! Самая то, что искала. Год назад вы мне помогли, и снова все позабылось. ❤❤❤❤❤❤

[ИванКузнецов-удш]

Подписался, очень понятно без воды, по факту, и хорошая подача, однозначно лайк

[bluendart]

Мне нравится понимать самую первую формулу, т.е. (вектор a) * (вектор b) = x*x1 + y*y1, представляя один из векторов в виде матрицы, в которой оба единичных вектора лежат на одной оси (их длины равны соответственно координатам представленного вектора). Умножая эту матрицу на другой вектор, мы как бы удлиним его в пропорции этой матрицы, и длина получившегося вектора будет равна x*x1 + y*y1 (по правилам умножения матрицы на вектор).

[soranex]

1 курс вуза, думал, что смотрю какое то объяснение уже из курса ангема, оказалось геометрия 9 класс💀

[Serjious_m]

в счете русов умножение - действие прекрасное, в математике сложение - очень вещь опасная

[ferum]

Добрий день. Натрапив на це відео коли шукав пояснення формули |a|*|b| * cos a. Завдяки цій формулі в мене вийшло вивести іншу формулу для скалярного добутку – ax*bx+ay*by. Вдалось вивести таким чином що вектори які множаться один на одного були розкладені як сума базисних векторів помножених на певний скаляр, тобто, наприклад вектор a розкладено як Xa*i + Ya*j де j та i базисні ортонормовані вектори з координатами (0;1) та (1;0) відповідно. Таким чином було розкладено вектор b як Xb*i + Yb*j. Тобто вектор a * вектор b = Xa*i+Ya*j * Xb*i+Yb*j. Далі користуючись властивостями лінійного простору (дистрибутивністью та комутативність) а також використовуючи формулу |i|*|j| * cos a = 0 та |i| * |i| * cos a' = 1 все було зведено до тої самої формули де скалярний добуток векторів a і b дорівнює Xa*Xb+YaYb. Так от, у вас ця формула була написана відразу як якась аксіома, чому так? Якщо наприклад при множенні двох натуральних чисел дія множення обозначає скільки разів певне число додається на себе, тобто 3*3 це значить що трійка три рази додається то що значить помножити вектор на вектор? Інше джерело, де я навчився виводити формулу скалярного добутку Xa*Xb+Ya*Yb при доведенні цієї формули користувалося формулою з добутком модулів який множиться на косинус кута між ними. Як вивести формулу з модулями і кутом між ними, якщо не знати формули Xa*Xb+Ya*Yb на яку ви спиралися в даному відео при доказі формули з модулями і кутом між ними. Якщо через певні причини не можете відповісти, то будь ласка, якщо можете, дайте посилання з розбором на цю тему. Дякую

[ПетроваВероника-ми]

И всё таки до конца не понятно, что это векторное произведение означает, как его понять ментально?

[vladwilliams]

Привет! Был бы рад если бы ты сделал геометрию 9 класса за 1 час! 7 есть, 8 есть, а вот 9 нет